
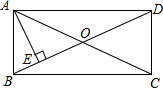
 如图,矩形ABCD的对角线AC,BD交于点O,AE⊥BD于点E,且∠DAE:∠BAE=2:1,AE=$\sqrt{3}$,则矩形ABCD的面积是4$\sqrt{3}$.
如图,矩形ABCD的对角线AC,BD交于点O,AE⊥BD于点E,且∠DAE:∠BAE=2:1,AE=$\sqrt{3}$,则矩形ABCD的面积是4$\sqrt{3}$. 分析 由矩形的性质和已知条件求出∠AOE=30°,由直角三角形的性质得出AD=2AE=2$\sqrt{3}$,求出AB=$\frac{\sqrt{3}}{3}$AD=2,即可得出矩形ABCD的面积.
解答 解:∵四边形ABCD是矩形,
∴∠BAD=90°,
∵∠DAE:∠BAE=2:1,
∴∠BAE=30°,∠DAE=60°,
∵AE⊥BD,
∴∠AOE=30°,
∴AD=2AE=2$\sqrt{3}$,
∴AB=$\frac{\sqrt{3}}{3}$AD=2,
∴矩形ABCD的面积=AD•AB=4$\sqrt{3}$;
故答案为:4$\sqrt{3}$.
点评 本题考查矩形的性质、直角三角形的性质、三角函数、矩形面积的计算;熟练掌握矩形的性质和直角三角形的性质是解决问题的关键.


科目:初中数学 来源: 题型:解答题
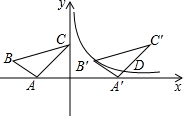 如图,△ABC的顶点A,C落在坐标轴上,且顶点B的坐标为(-5,2)将△ABC沿x轴向右平移7个单位得到△A′B′C′,点B′恰好在反比例函数y=$\frac{k}{x}$的图象上,且反比例函数图象与A′C′相交于点D.
如图,△ABC的顶点A,C落在坐标轴上,且顶点B的坐标为(-5,2)将△ABC沿x轴向右平移7个单位得到△A′B′C′,点B′恰好在反比例函数y=$\frac{k}{x}$的图象上,且反比例函数图象与A′C′相交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 把△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得到△AB′C′,即如图,∠BAB′=θ,$\frac{AB′}{AB}$=$\frac{B′C′}{BC}$=$\frac{AC′}{AC}$=n,我们将这种变换记为[θ,n].△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,那么θ=72°,n=$\frac{1+\sqrt{5}}{2}$.
把△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得到△AB′C′,即如图,∠BAB′=θ,$\frac{AB′}{AB}$=$\frac{B′C′}{BC}$=$\frac{AC′}{AC}$=n,我们将这种变换记为[θ,n].△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,那么θ=72°,n=$\frac{1+\sqrt{5}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
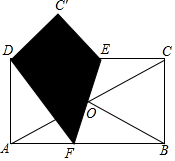 如图是一个矩形纸片ABCD,连接AC,DB交于点O,且AC=4$\sqrt{5}$,若AD:AB=1:2,将纸片折叠使B与D重合,折痕为EF,求折叠后纸片重合部分的面积.
如图是一个矩形纸片ABCD,连接AC,DB交于点O,且AC=4$\sqrt{5}$,若AD:AB=1:2,将纸片折叠使B与D重合,折痕为EF,求折叠后纸片重合部分的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
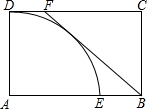 如图,矩形ABCD,AB=3,AD=2,以点A为圆心,AD长为半径的DE交AB于E,DF=0.8,判断直线BF与DE所在的圆的位置关系.
如图,矩形ABCD,AB=3,AD=2,以点A为圆心,AD长为半径的DE交AB于E,DF=0.8,判断直线BF与DE所在的圆的位置关系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
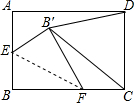 如图,在矩形ABCD中,AB=6,BC=8,点E为AB的中点,点F为BC边上任意一点,将△BEF沿EF翻折,点B的对应点为B′,则当△B′CD面积最小时折痕EF的长为3$\sqrt{2}$.
如图,在矩形ABCD中,AB=6,BC=8,点E为AB的中点,点F为BC边上任意一点,将△BEF沿EF翻折,点B的对应点为B′,则当△B′CD面积最小时折痕EF的长为3$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com