
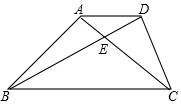
 已知如图,在等腰Rt△ABC中,AB=AC,在等腰△BCD中,BC=BD,BD、AC相交于E,AD∥BC,求证:CD=CE.
已知如图,在等腰Rt△ABC中,AB=AC,在等腰△BCD中,BC=BD,BD、AC相交于E,AD∥BC,求证:CD=CE. 分析 作梯形的双高,把四边形问题转化为三角形问题,只要证明∠DBM=30°即可解决问题.
解答 证明: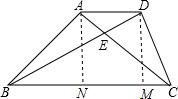 作AN⊥BC于N,DM⊥BC于M,则AN∥DM,
作AN⊥BC于N,DM⊥BC于M,则AN∥DM,
∵AD∥BC,
∴四边形ANMD是平行四边形,
∵∠ANM=90°,
∴DM=AN,
∵△ABC为等腰直角三角形,
∴BC=2AN=2DM,
∵BD=BC,
∴BD=2DM,
∵∠DMB为直角,
∴∠DBC=30°,
∴∠DEC=45°+30°=75°,
∵BD=BC,
∴∠BDC=$\frac{1}{2}$(180°-∠DBC)=$\frac{1}{2}$(180°-30°)=75°,
∴∠DEC=∠EDC,
∴CE=CD.
点评 本题考查了等腰直角三角形性质,含30度角的直角三角形性质,矩形的性质和判定,三角形的内角和定理的应用,解题的关键是学会添加常用辅助线,把四边形问题转化为三角形问题解决问题,属于中考常考题型.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在长为70米,宽为40米的长方形空地中,张老板想在上面修建焯天茶餐厅和子欣西餐厅,两所餐厅的四周铺上等宽的小路隔开,如果小路的面积占总面积的八分之一,求小路的宽度是多少?
如图,在长为70米,宽为40米的长方形空地中,张老板想在上面修建焯天茶餐厅和子欣西餐厅,两所餐厅的四周铺上等宽的小路隔开,如果小路的面积占总面积的八分之一,求小路的宽度是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
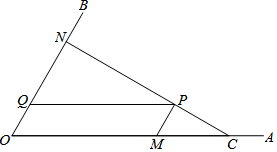 如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.
如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com