
已知:抛物线y=x2+bx+c经过点(2,-3)和(4,5).
(1)求抛物线的表达式及顶点坐标;
 (2)将抛物线沿x轴翻折,得到图象G,
(2)将抛物线沿x轴翻折,得到图象G,
求图象G的表达式;
(3)在(2)的条件下,当-2<x<2时,
直线y=m与该图象有一个公共点,
求m的值或取值范围.
解:(1)把(2,-3)和(4,5)分别代入y=x²+bx+c
得: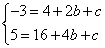 ,解得:
,解得: ,
,
∴抛物线的表达式为:y=x²-2x-3. ………………1分.
 ∵y=x²-2x-3=(x-1)2-4.
∵y=x²-2x-3=(x-1)2-4.
∴顶点坐标为(1,-4). ………………………2分.
(2)∵将抛物线沿x轴翻折,
得到图象G与原抛物线图形关于x轴对称,
∴图像G的表达式为:y=-x²+2x+3. ………3分.
(3)如图,当0≤x<2时,y=m过抛物线顶点(1,4)时,
直线y=m与该图象有一个公共点,
此时y=4,∴m=4. ………………4分
当-2<x<0时,直线y=m与该图象有一个公共点,
当y=m过抛物线上的点(0,3)时, y=3,∴m=3.
当y=m过抛物线上的点(-2,-5)时, y=-5,∴m=-5.
∴-5<m<3.
综上:m的值为4,或-5<m≤3. …………………………………5分.


科目:初中数学 来源: 题型:
以下列各组线段为边,能组成三角形的是( )
A.1cm,2cm,4cm B.4cm,6cm,8cm C.5cm,6cm,12cm D.2cm,3cm,5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
学习相似三角形和解直角三角形的相关内容后,张老师请同学们交流这样的一个问题:“如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形是否相似?”.那么你认为△A1B1C1和△A2B2C2 .(填相似或不相似);理由是 .
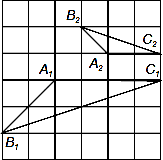
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com