
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
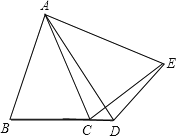
(1)如图1,当点D在线段BC上,如果∠BAC=90,则∠BCE 度;
(2)设∠BAC=,∠BCE=.
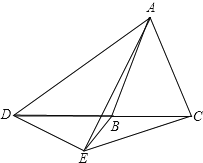
①如图2,当点D在线段BC上移动,则,之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则,之间有怎样的数量关系?请直接写出你的结论,不必说明理由.

【答案】(1)、90°;(2)、①、α+β=180°;理由见解析;②、当点D在射线BC上时,α+β=180°;
当点D在射线BC的反向延长线上时,α=β.
【解析】
试题分析:(1)、根据∠BAC=∠DAE得出∠BAD=∠CAE,然后利用SAS判定△ABD和△ACE全等,从而得出∠B=∠ACE,则∠B+∠ACB=∠ACE+∠ACB,从而得出∠BCE=90°;(2)、①、、根据∠BAC=∠DAE得出∠BAD=∠CAE,然后利用SAS判定△ABD和△ACE全等,从而得出∠B=∠ACE,则∠B+∠ACB=∠ACE+∠ACB,从而得出α+β=180°;②、根据题意分别画出两个图形,然后分别进行计算得出答案,当点D在射线BC上时,α+β=180°;当点D在射线BC的反向延长线上时,α=β.
试题解析:(1)、90°.
∵∠BAC=∠DAE, ∴∠BAC-∠DAC=∠DAE-∠DAC. 即∠BAD=∠CAE.
在△ABD与△ACE中,AB=AC,∠BAD=∠CAE,AD=AE ∴△ABD≌△ACE(SAS),
∴∠B=∠ACE. ∴∠B+∠ACB=∠ACE+∠ACB, ∴∠BCE=∠B+∠ACB, 又∵∠BAC=90° ∴∠BCE=90°
(2)、①α+β=180°,
∵∠BAC=∠DAE, ∴∠BAD+∠DAC=∠EAC+∠DAC. 即∠BAD=∠CAE.
在△ABD与△ACE中,AB=AC,∠BAD=∠CAE,AD=AE ∴△ABD≌△ACE(SAS), ∴∠B=∠ACE.
∴∠B+∠ACB=∠ACE+∠ACB. ∴∠B+∠ACB=β, ∵α+∠B+∠ACB=180°, ∴α+β=180°;
②、当点D在射线BC上时,α+β=180°;
当点D在射线BC的反向延长线上时,α=β.


科目:初中数学 来源: 题型:
【题目】今年,6月12日为端午节.在端午节前夕,三位同学到某超市调研一种进价为2元的粽子的销售情况.请根据小丽提供的信息,解答小华和小明提出的问题.

(1)小华的问题解答:
(2)小明的问题解答:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市2004年接待境外游客人数和旅游直接创汇名列全省前茅,实现旅游直接创汇29092700美元,这个数用科学计数法表示是______________美元(保留到十万位)
查看答案和解析>>
科目:初中数学 来源: 题型:
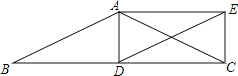
【题目】如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD、CE.
(1)求证:△ACD≌△EDC;
(2)若点D是BC中点,说明四边形ADCE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的个数是( )
(1)连接两点之间的线段叫两点间的距离;
(2)两点之间,线段最短;
(3)若AB=2CB,则点C是AB的中点;
(4)角的大小与角的两边的长短无关.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分) 若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“兄弟二次函数”.
(1)请写出两个为“兄弟二次函数”的函数;
(2)已知关于x的二次函数y1=2x2﹣4mx+2m2+1和y2=ax2+bx+5,其中y1的图象经过点A(1,1),若y1+y2与y1为“兄弟二次函数”,求函数y2的表达式,并直接写出当0≤x≤3时,y2的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com