
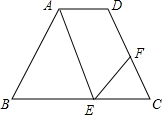
 如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°
如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
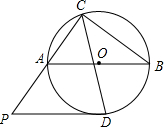 如图,△ABC内接于⊙O,且AB为⊙O的直径,过CA延长线上点P作⊙O的切线PD.切点为D,且PD∥AB.
如图,△ABC内接于⊙O,且AB为⊙O的直径,过CA延长线上点P作⊙O的切线PD.切点为D,且PD∥AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
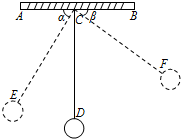 如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E、F两点的俯角分别为∠ACE=α,∠BCF=β,这时点F相对于点E升高了acm.求该摆绳CD的长度.(用含a、α、β的式子表示)
如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E、F两点的俯角分别为∠ACE=α,∠BCF=β,这时点F相对于点E升高了acm.求该摆绳CD的长度.(用含a、α、β的式子表示)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
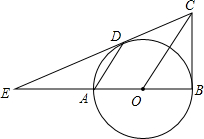 如图,已知AB是⊙O的直径,BC⊥AB,连接OC,弦AD∥OC,直线CD交BA的延长线于点E.
如图,已知AB是⊙O的直径,BC⊥AB,连接OC,弦AD∥OC,直线CD交BA的延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
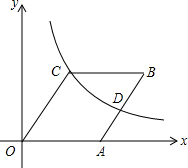 如图,在菱形OABC中点A在x轴的正半轴上,点B坐标为(8,4)双曲线y=$\frac{k}{x}$(k>0)经过点C,交AB于点D.
如图,在菱形OABC中点A在x轴的正半轴上,点B坐标为(8,4)双曲线y=$\frac{k}{x}$(k>0)经过点C,交AB于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com