
| A. | 平行 | B. | 垂直 | C. | 相等 | D. | 无法确定 |
分析 首先根据题意画出图形,写出已知与要求的结论,利用平行线的性质得到∠BGN+∠DNG=180°,再利用角平分线可以得到∠MGN=$\frac{1}{2}$∠BGN,∠GNM=$\frac{1}{2}$∠GND,从而得到∠GMN=90°,可得到GM与NM的关系是垂直.
解答 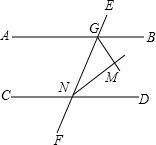 解:由题意得;已知:AB∥CD,GM平分∠BGN,MN平分∠GND,MN与GM交于点M.
解:由题意得;已知:AB∥CD,GM平分∠BGN,MN平分∠GND,MN与GM交于点M.
求GM与NM的关系?
GM与NM的关系是垂直.
理由如下;∵AB∥CD,
∴∠BGN+∠DNG=180°,
∵GM平分∠BGN,MN平分∠GND,
∴∠MGN=$\frac{1}{2}$∠BGN,∠GNM=$\frac{1}{2}$∠GND,
∴∠MGN+∠GNM=$\frac{1}{2}$∠BGN+$\frac{1}{2}$∠GND=$\frac{1}{2}$(∠BGN+∠GND)=$\frac{1}{2}$×180°=90°,
∴∠GMN=180°-90°=90°,
∴GM⊥NM.
故选:B.
点评 此题主要考查了平行线的性质与角平分线的性质,正确观画出图形,写出已知,是解题的关键.


科目:初中数学 来源: 题型:填空题
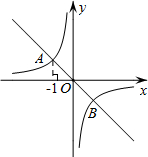 如图,在平面直角坐标系xOy中,一次函数y=-x的图象与反比例函数y=$\frac{k}{x}$图象交于A,B两点,若点P在y轴上,且满足以点A,B,P为顶点的三角形是直角三角形,则点P的坐标是(0,$\sqrt{2}$)或(0,-$\sqrt{2}$)或(0,2)或(0,-2).
如图,在平面直角坐标系xOy中,一次函数y=-x的图象与反比例函数y=$\frac{k}{x}$图象交于A,B两点,若点P在y轴上,且满足以点A,B,P为顶点的三角形是直角三角形,则点P的坐标是(0,$\sqrt{2}$)或(0,-$\sqrt{2}$)或(0,2)或(0,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
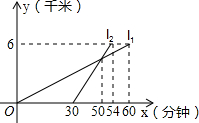 某校八年级同学到距学校6千米的郊外春游,一部分同学步行,另一部分同学骑自行车,他们都沿相同路线前往.如图,已知a、b分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象,请你根据图中提供的信息,写出三个正确结论.
某校八年级同学到距学校6千米的郊外春游,一部分同学步行,另一部分同学骑自行车,他们都沿相同路线前往.如图,已知a、b分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象,请你根据图中提供的信息,写出三个正确结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com