
【题目】如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长为 . 
【答案】![]()
【解析】:∵△ABC是等边三角形,
∴AB=BC=AC=3,∠B=∠C=60°,
∴∠BAP+∠APB=180°-60°=120°,
∵∠APD=60°,
∴∠APB+∠DPC=180°-60°=120°,
∴∠BAP=∠DPC ,
即∠B=∠C , ∠BAP=∠DPC ,
∴△BAP∽△CPD ,
∴ ![]() =
= ![]() ,
,
∵AB=BC=3,CP=BC-BP=3-1=2,BP=1,
即 ![]() =
= ![]() ,
,
解得:CD= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】根据题目的已知条件,利用相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,为了测量某风景区内一座塔AB的高度,小明分别在塔的对面一楼房CD的楼底C,楼顶D处,测得塔顶A的仰角为45°和30°,已知楼高CD为10m,求塔的高度(结果精确到0.1m).(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD中,E、F分别是边BC , CD上的点,且EF∥BD , AE、AF分别交BD与点G和点H , BD=12,EF=8.求: 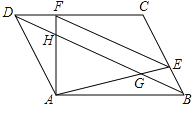
(1)![]() 的值;
的值;
(2)线段GH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D , E分别在AB , AC上,DE∥BC , AD=CE . 若AB:AC=3:2,BC=10,则DE的长为( ) 
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,E、D分别是AC、BC的中点,AD、BE交于点O , 则S△DOE:S△AOB=( ) 
A.1:2
B.2:3
C.1:3
D.1:4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,过点B的直线与对角线AC、边AD分别交于点E和F . 过点E作EG∥BC , 交AB于G , 则图中相似三角形有( ) 
A.4对
B.5对
C.6对
D.7对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程x2-x-3=0的较小根为x1 , 则下面对x1的估计正确的是( )
A.-2< x1<-1
B.-3< x1<-2
C.2< x1<3
D.-1< x1<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com