Question

【题目】已知：如图，在平行四边形ABCD中，E、F分别是边BC ， CD上的点，且EF∥BD ， AE、AF分别交BD与点G和点H ， BD=12，EF=8．求：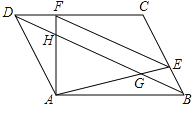
（1） 的值；
（2）线段GH的长．

Answer 1

【答案】
（1）解答：∵EF∥BD，

∴ ，

∵BD=12，EF=8，

∴ ，

∴ ，

∵四边形ABCD是平行四边形，∴AB=CD，

∴ ；

（2）解答：∵DF∥AB，

∴ ，

∴ ，

∵EF∥BD，

∴ ，

∴ ，

∴GH=6．

【解析】分析：（1）根据EF∥BD ， 则 ，再利用平行四边形的性质求得 的值；（2）利用DF∥AB ， 则 ，进而得出 ，即可求出GH ．
【考点精析】根据题目的已知条件，利用平行四边形的性质和平行线分线段成比例的相关知识可以得到问题的答案，需要掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分；三条平行线截两条直线，所得的对应线段成比例．