
如图,抛物线y=x2+mx+(m﹣1)与x轴交于点A(x1,0),B(x2,0),x1<x2,与y轴交于点C(0,c),且满足x12+x22+x1x2=7.

(1)求抛物线的解析式;
(2)在抛物线上能不能找到一点P,使∠POC=∠PCO?若能,请求出点P的坐标;若不能,请说明理由
1)抛物线的解析式是y=x2-2x-3;(2)能;点P的坐标是(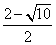 ,-
,-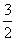 ),(
),( ,-
,-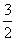 ).
).
【解析】(1)依题意:x1+x2=-m,x1x2=m-1,∵x12+x22+x1x2=7,∴( x1+x2)2-x1x2=7,
x1+x2)2-x1x2=7,
∴(-m)2-(m-1)=7,即m2-m-6=0,解得m1=-2,m2=3,∵c=m-1<0,∴m=3不合题意
∴m=-2抛物线的解析式是y=x2-2x-3;
(2)能
如图,设P是抛物线上的一点,连接PO,PC,过点P作y轴的垂线,垂足为D.
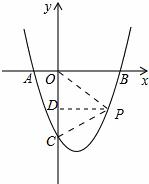
若∠POC=∠PCO,则PD应是线段OC的垂直平分线,∵C的坐标为(0,-3),
∴D的坐标为(0,-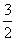 ),∴P的纵坐标应是-
),∴P的纵坐标应是-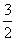 ,令x2-2x-3=-
,令x2-2x-3=-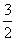 ,解得,x1=
,解得,x1=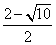 ,x2=
,x2= ,因此所求点P的坐标是(
,因此所求点P的坐标是(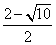 ,-
,-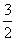 ),(
),( ,-
,-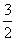 ).
).


科目:初中数学 来源: 题型:
C.
【解析】如果将图①看作是铺成的一个1×1的正方形图案,图②看作是铺成的一个2×2的正方形图案,图③看作是铺成的一个3×3的正方形图案,图④看作是铺成的一个4×4的正方形图案,那么根据给出的四个图形的规律可以知道,组成大正方形的每个小正方形上有一个完整的圆,因此圆的数目是大正方形边长的平方;又每四个小正方形组成一个完整的圆,这样的圆的个数是大正方形的边长减1的平方,从而可得第10个图中完整的圆共有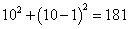 个.
个.
故选C.
查看答案和解析>>
科目:初中数学 来源: 题型:
“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗,我市某食品厂为了解市民对去年销售量较好的肉馅粽、豆沙粽、红枣粽、蛋黄馅粽(以下分别用A、B、C、D表示这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查结果绘制成如下两幅统计图.
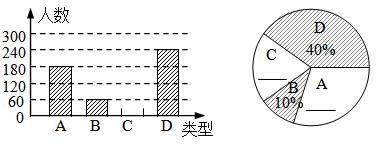
请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将不完整的条形图补充完整.
(3)若居民区有8000人,请估计爱吃D粽的人数?
(4)若有外型完全相同的A、B、C、D粽各一个煮熟后,小王吃了俩个,用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com