【题目】如图，点 O 为直线 AB 上一点，过点 O 作射线 OC，使∠BOC＝135°，将一个含 45°角的直角三角尺的一个顶点放在点 O 处，斜边 OM 与直线 AB 重合，另外两条直角边都在直线 AB 的下方．

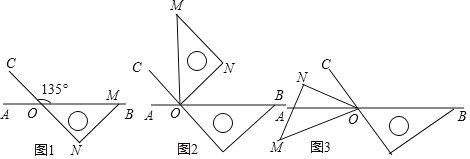
（1）将图 1 中的三角尺绕着点 O 逆时针旋转 90°，如图 2 所示，此时∠BOM＝ 度（答案直接填写在答题卡的横线上）；在图 2 中，OM 是否平分∠CON ? 请说明理由；

（2）紧接着将图 2 中的三角板绕点 O 逆时针继续旋转到图 3 的位置所示，使得 ON 在∠AOC 的内部，请探究：∠AOM 与∠CON 之间的数量关系，并说明理由；

（3）将图 1 中的三角板绕点 O 按每秒 5°的速度沿逆时针方向旋转一周，在旋转的过程中， 第 t 秒时，直线 ON 恰好平分锐角∠AOC，请你直接写出t 的值为多少．

参考答案：

【答案】（1）∠BOM=90°；M 是否平分∠CON，理由见解析；（2）∠AOM=∠CON，理由见解析；（3）4.5秒或40.5秒

【解析】

（1）利用旋转的性质可得∠BOM的度数，然后计算∠MOC的度数判断OM是否平分∠CON；

（2）利用∠AOM=45°-∠AON和∠NOC=45°-∠AON可判断∠AOM与∠CON之间的数量关系；

（3）ON旋转22.5度和202.5度时，ON平分∠AOC，然后利用速度公式计算t的值．

解：（1）如图2，由旋转的性质可知∠BOM=90°，

OM平分∠CON．理由如下：

∵∠BOC=135°，

∴∠MOC=135°-90°=45°，

而∠MON=45°，

∴∠MOC=∠MON；

（2）∠AOM=∠CON．

理由如下：如图3，

∵∠MON=45°，

∴∠AOM=45°-∠AON，

∵∠AOC=45°，

∴∠NOC=45°-∠AON，

∴∠AOM=∠CON；

（3）t=×45°÷5°=4.5（秒）或t=（180°+22.5°）÷5°=40.5（秒）．

故答案为90°；4.5秒或40.5秒．

关闭