
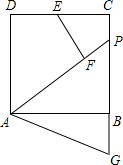
 如图,P为正方形ABCD边BC上一点,F在AP上,且AF=AD,EF⊥AP交CD于点E,G为CB延长线上一点,BG=DE.
如图,P为正方形ABCD边BC上一点,F在AP上,且AF=AD,EF⊥AP交CD于点E,G为CB延长线上一点,BG=DE.分析 (1)连接AE,先由HL证明Rt△ADE≌Rt△AFE,得出∠DAE=∠FAE=$\frac{1}{2}$∠DAP,再证明△ADE≌△ABG,得出∠DAE=∠BAG,即可得出结论;
(2)设CP=x,作EH∥AD交AB于H,连接EF;先证明EH是梯形ADCP的中位线,得出EH=$\frac{1}{2}$(4+x),再证明∠AEP=90°,由直角三角形斜边上的中线性质得出EH=$\frac{1}{2}$AP,在直角三角形ABP中,根据勾股定理求出x,即可得出AP.
解答 (1)证明:连接AE,如图所示:
∵四边形ABCD是正方形,
∴∠D=∠ABC=90°,AD=AB,
∴∠ABG=90°,
∵EF⊥AP,
∴∠AFE=90°,
在Rt△ADE和Rt△AFE中,
$\left\{\begin{array}{l}{AE=AE}\\{AD=AF}\end{array}\right.$,
∴Rt△ADE≌Rt△AFE(HL),
∴DE=EF,∠DAE=∠FAE=$\frac{1}{2}$∠DAP,
在△ADE和△ABG中,$\left\{\begin{array}{l}{AD=AB}&{\;}\\{∠ADE=∠ABG}&{\;}\\{DE=BG}&{\;}\\{\;}&{\;}\end{array}\right.$,
△ADE≌△ABG(SAS),
∴∠DAE=∠BAG=$\frac{1}{2}$∠DAP,
∴∠PAG=∠BAP+∠BAG=∠BAP+$\frac{1}{2}$∠DAP;
(2)解:设CP=x,作EH∥AD交AB于H,连接EF;
则H是AP的中点,EH是梯形ADCP的中位线,
∴EH=$\frac{1}{2}$(4+x),
∵由(1)Rt△ADE≌Rt△AFE,
∴∠AED=∠AEF,
同理:∠CEP=∠FEP,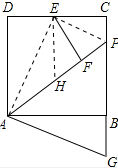
∴∠AEP=90°,
∴EH=$\frac{1}{2}$AP,
∴AP=4+x,
在Rt△ABP中,PB=4-x,
根据勾股定理得:AB2+PB2=AP2,
即42+(4-x)2=(4+x)2,
解得:x=1,
∴AP=5.
方法二:∵DE=EC═EF=2,EF=EF,
∴Rt△EPC≌Rt△EPF,
∴PC=PF,
由△EPC∽△AED,可得PC=PF=1,
∴AP=AF+PF=4+1=5.
点评 本题考查了全等三角形的判定与性质、正方形的性质、梯形的中位线、勾股定理的运用;本题有一定难度,需要通过作辅助线设出未知数,通过勾股定理求出结果.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
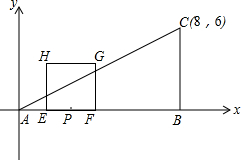 在Rt△ABC中,∠ABC=90°,以A为坐标原点,AB所在直线为x轴,建立平面直角坐标,且C坐标(8,6),点P在AB上,AP=2,E、F同时从点P出发,分别沿PA、PB以每秒1个单位的速度向A、B匀速运动,点E到达A后立即以原速沿AB向B运动,点E再次返回点P停止,点F也随之停止运动,在点E、F运动过程中,以EF为边向上做正方形EFGH,设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠面积为S.
在Rt△ABC中,∠ABC=90°,以A为坐标原点,AB所在直线为x轴,建立平面直角坐标,且C坐标(8,6),点P在AB上,AP=2,E、F同时从点P出发,分别沿PA、PB以每秒1个单位的速度向A、B匀速运动,点E到达A后立即以原速沿AB向B运动,点E再次返回点P停止,点F也随之停止运动,在点E、F运动过程中,以EF为边向上做正方形EFGH,设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com