
分析 先变形得到原式=[($\sqrt{3}$-$\sqrt{2}$)+2$\sqrt{6}$][($\sqrt{3}$-$\sqrt{2}$)-2$\sqrt{6}$],然后利用平方差公式和完全平方公式进行计算.
解答 解:原式=[($\sqrt{3}$-$\sqrt{2}$)+2$\sqrt{6}$][($\sqrt{3}$-$\sqrt{2}$)-2$\sqrt{6}$]
=($\sqrt{3}$-$\sqrt{2}$)2-(2$\sqrt{6}$)2
=5-2$\sqrt{6}$-24
=-19-2$\sqrt{6}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.


科目:初中数学 来源: 题型:选择题
| A. | 1,$\sqrt{5}$,2 | B. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | C. | 3,4,5 | D. | 32,42,52 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
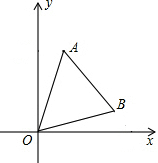 如图,平面直角坐标系中,A(1,4),B(3,1)
如图,平面直角坐标系中,A(1,4),B(3,1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
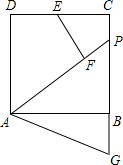 如图,P为正方形ABCD边BC上一点,F在AP上,且AF=AD,EF⊥AP交CD于点E,G为CB延长线上一点,BG=DE.
如图,P为正方形ABCD边BC上一点,F在AP上,且AF=AD,EF⊥AP交CD于点E,G为CB延长线上一点,BG=DE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
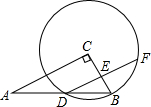 如图,在Rt△ABC中,∠C=90°,AB=10,若以点C为圆心,CB长为半径的圆恰好经过AB的中点D,弦DF∥AC,则DF的长为5$\sqrt{3}$.
如图,在Rt△ABC中,∠C=90°,AB=10,若以点C为圆心,CB长为半径的圆恰好经过AB的中点D,弦DF∥AC,则DF的长为5$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
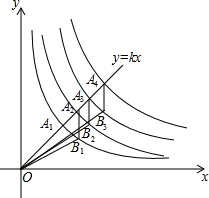 如图,正比例函数y=kx(k>0)的图象与反比例函数y1=$\frac{1}{x}$,y2=$\frac{2}{x}$,…,y2014=$\frac{2014}{x}$的图象在第一象限内分别交于点A1,A2,…A2014.点B1,B2,…,B2013分别在反比例函数y1=$\frac{1}{x}$,y2=$\frac{2}{x}$,…,y2013=$\frac{2013}{x}$的图象上,且A2B1,A3B2,…,A2014B2013分别与y轴平行,连接OB1,OB2,…,OB2013,则△OA2B1,△OA3B2,…,△OA2014B2013的面积之和为( )
如图,正比例函数y=kx(k>0)的图象与反比例函数y1=$\frac{1}{x}$,y2=$\frac{2}{x}$,…,y2014=$\frac{2014}{x}$的图象在第一象限内分别交于点A1,A2,…A2014.点B1,B2,…,B2013分别在反比例函数y1=$\frac{1}{x}$,y2=$\frac{2}{x}$,…,y2013=$\frac{2013}{x}$的图象上,且A2B1,A3B2,…,A2014B2013分别与y轴平行,连接OB1,OB2,…,OB2013,则△OA2B1,△OA3B2,…,△OA2014B2013的面积之和为( )| A. | 1007 | B. | $\frac{2013}{2}$ | C. | 1006 | D. | $\frac{2011}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
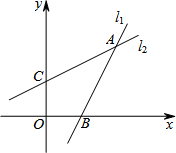 如图,直线l1:y=kx+b与x轴交于点B(1,0),直线l2:$y=\frac{1}{2}x+1$与y轴交于点C,这两条直线交于点A(2,a).
如图,直线l1:y=kx+b与x轴交于点B(1,0),直线l2:$y=\frac{1}{2}x+1$与y轴交于点C,这两条直线交于点A(2,a).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com