
【题目】∠1=∠2,∠3=∠B,FG⊥AB于G,猜想CD与AB的关系,并证明你的猜想.
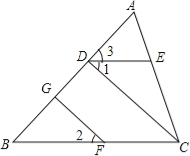
【答案】垂直,证明见解析
【解析】试题分析:根据∠3=∠B得出ED∥BC,根据FG⊥AB得出∠AGF=90°,根据外角的性质得出∠AGF=∠B+∠2,结合∠ADC=∠1+∠3,∠1=∠2,∠3=∠B从而得出∠ADC=∠AGF=90°,从而得到垂直.
试题解析:猜想CD⊥AB.
理由如下: ∵∠3=∠B(已知),∴ED∥BC(同位角相等,两直线平行).
∵FG⊥AB(已知),∴∠AGF=90°(垂直定义).
∵∠AGF是△BFG的一个外角, ∴∠AGF=∠B+∠2(三角形的一个外角等于和它不相邻的两个内角的和).
∵∠ADC=∠1+∠3,而∠1=∠2,∠3=∠B, ∴∠ADC=∠AGF=90°(等量代换).
∴CD⊥AB(垂直定义).


科目:初中数学 来源: 题型:
【题目】如图,△ABD中,∠BAD=90°,AB=AD,△ACE中,∠CAE=90°,AC=AE。

(1)求证:DC=BE;
(2)试判断∠AFD和∠AFE的大小关系,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在日常生活中如取款、上网等都需要密码,有一种用“因式分解”法产生的密码记忆方便.原理是:如对于多项式x4﹣y4,因式分解的结果是(x﹣y)(x+y)(x2+y2),若取x=9,y=9时,则各个因式的值是:(x﹣y)=0,(x+y)=18,(x2+y2)=162,于是就可以把“018162”作为一个六位数的密码.对于多项式x3﹣xy2,取x=20,y=10,用上述方法产生的密码不可能是( )
A.201010 B.203010 C.301020 D.201030
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,
∠BAD=45°,AD与BE交于点F,连接CF.
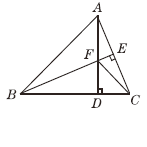
(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com