
���� ��1����A��x��0������OA=-x��OB=-2x��OC=-2x-2�������ɵ�B��-2x��0����C��0��-2x-2����Ȼ�����OC-OA=2���ɵ�x=-4�������ɵõ�C�����ꣻ
��2���ɣ�1����֪AB=OA+OB=12���ɵ�Q�ӵ�B������ÿ��3����λ���ٶ���BA���յ�A�����˶�������Q�����յ�Aʱ����P��Q��ֹͣ�˶����ɵ�t�����ֵΪ4�룬Ȼ�����P��Q��������ʱ��t��ֵΪ��12�£�1+3��=3�룬Ȼ�������������ۼ��ɣ���0��t��3����3��t��4��
��3����OΪPQ�е㣬��֪0��t��3��OP=OQ����OA-AP=OB-BP����������t��ֵ��Ȼ�������������ۼ��ɣ��ٵ�M��x���Ϸ����ڵ�M��x���·���
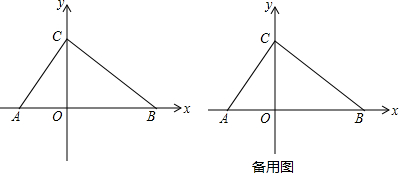
��� �⣺��1���ߵ�A��x�Ḻ�����ϣ���B��C�ֱ���x�ᡢy���������ϣ�OB=2OA��OB-OC=OC-OA=2��
��A��x��0����
��OA=-x��OB=-2x��OC=-2x-2��
��B��-2x��0����C��0��-2x-2����
��OC-OA=2��
��-2x-2-��-x��=2��
��ã�x=-4��
��OA=4��OB=8��OC=6����A��������-4��0������B��������8��0������C��������0��6����
��2���ɣ�1��֪��AB=OA+OB=12��
�ߵ�P�ӵ�A������ÿ��1����λ���ٶ���AB���B�����˶���ͬʱ��Q�ӵ�B������ÿ��3����λ���ٶ���BA���յ�A�����˶���
���P�˶���ʱ��Ϊt��t��0����ʱ��AP=t��BQ=3t��
��P��Q��������ʱ��t��ֵΪ��12�£�1+3��=3�룬
�ߵ���Q�����յ�Aʱ����P��Q��ֹͣ�˶���
��t�����ֵΪ12��3=4��
�ٵ�0��t��3ʱ����ͼ1��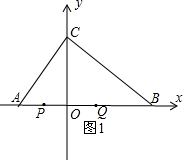
PQ=AB-AP-QB=12-t-3t=12-4t��
��y=12-4t��0��t��3����
�ڵ�3��t��4ʱ����ͼ2��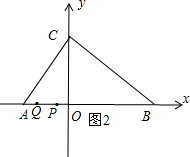
PQ=AP+BQ-AB=4t-12��
��y=4t-12��3��t��4����
��3������tֵʹ��OΪPQ�е㣬
�ߵ�OΪPQ�е㣬
��0��t��3��OP=OQ����OA-AP=OB-BQ��
��4-t=8-3t��
��ã�t=2��
��t=2ʱ��AP=2��OP=2��OQ=2��PQ=4��PM=PQ=4��
�ٵ�M��x���Ϸ�ʱ����ͼ3��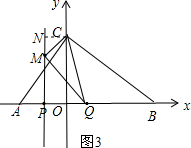
����C��CN��PM���ã��ı���CNPQ�����Σ�
��S��CMQ=S����CNPQ-S��CNM-S��PQM��
��S��CMQ=$\frac{1}{2}$��CN+PQ����PN-$\frac{1}{2}$CN•MN-$\frac{1}{2}•$PM•PQ
=$\frac{1}{2}��$��OP+PQ����OC-$\frac{1}{2}$��OP����OC-PM��-$\frac{1}{2}$��4��4
=$\frac{1}{2}��$��2+4����6-$\frac{1}{2}��$2����6-4��-8
=18-2-8
=8��
�ڵ�M��x���·�����ͼ4��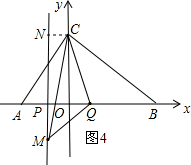
����C��CN��PM���ã��ı���CNPQ�����Σ�
��S��CMQ=S����CNPQ+S��PQM-S��CNM��
��S��CMQ=$\frac{1}{2}$��CN+PQ��•PN+$\frac{1}{2}$•PQ•PM-$\frac{1}{2}$•MN•CN
=$\frac{1}{2}��$��OP+PQ����OC+$\frac{1}{2}$��4��4-$\frac{1}{2}•$��OC+PM��•OP
=$\frac{1}{2}��$��2+4����6+8-$\frac{1}{2}��$��6+4����2
=$\frac{1}{2}��6��6$+8-$\frac{1}{2}��10��2$
=18+8-10
=16��
��������CMQ�������8��16��
���� ���⿼����������ͼ�ε����ʣ��ڣ�2������3�����ʽ���Ĺؼ��ǣ���������ۣ�2������0��t��3����3��t��4����3�����ٵ�M��x���Ϸ����ڵ�M��x���·���


 ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д�
ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д� â���̸����������������ϵ�д�
â���̸����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
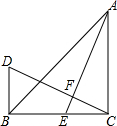 �ڡ�ABC�У���ACB=90�㣬AC=BC��CD��AE�ڵ�F��BD��BC�ڵ�B��AEΪBC���ϵ����ߣ���˵����AE=CD��
�ڡ�ABC�У���ACB=90�㣬AC=BC��CD��AE�ڵ�F��BD��BC�ڵ�B��AEΪBC���ϵ����ߣ���˵����AE=CD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
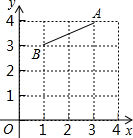 ��ͼ����ƽ��ֱ������ϵ�У����߶�AB�Ƶ�B��˳ʱ�뷽����ת90��õ��߶�A��B�����A�������Ϊ��2��1����
��ͼ����ƽ��ֱ������ϵ�У����߶�AB�Ƶ�B��˳ʱ�뷽����ת90��õ��߶�A��B�����A�������Ϊ��2��1�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
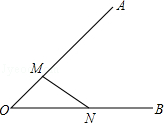 ��ͼ����ͼ������һ��P��ʹ��P���������߶�MNΪ����Բ��P����AOB���ߵľ�����ȣ�������ͼ�ۼ���д����������Ҫ���ó߹���ͼ��
��ͼ����ͼ������һ��P��ʹ��P���������߶�MNΪ����Բ��P����AOB���ߵľ�����ȣ�������ͼ�ۼ���д����������Ҫ���ó߹���ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
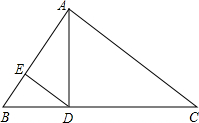 ��ͼ���ڡ�ABC�У���BAC=90�㣬AD��BC��D��DE��AB��E����AD=3��DE=2����AC=��������
��ͼ���ڡ�ABC�У���BAC=90�㣬AD��BC��D��DE��AB��E����AD=3��DE=2����AC=��������| A�� | $\frac{21}{2}$ | B�� | $\frac{\sqrt{15}}{2}$ | C�� | $\frac{9}{2}$ | D�� | $\sqrt{15}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com