
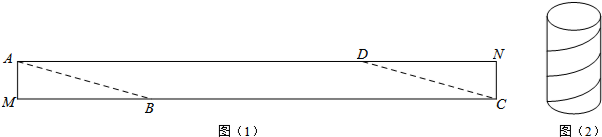
分析 根据圆柱体包装盒,高40cm,纸带在侧面缠绕四圈,正好将这个圆柱包装盒的侧面全部包贴满,可得出BF,AB的长度,由勾股定理得到AF的长度,即可得到结果.
解答 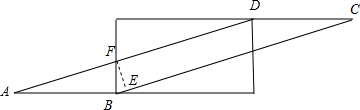 解:根据包贴方法可得展开图如下:
解:根据包贴方法可得展开图如下:
过点F作FE⊥BC于E,
∵纸带在侧面缠绕四圈,正好将这个三棱柱包装盒的侧面全部包贴满,
∵圆柱体的高40cm,
∴FB=$\frac{40}{3}$cm,AB=20,
在Rt△ABF中,AF=$\frac{20\sqrt{13}}{3}$,
∵DF=2AF=$\frac{40\sqrt{13}}{3}$,
∴AD=AF+DF=20$\sqrt{13}$,
故答案为;20$\sqrt{13}$.
点评 本题考查了平面展开图形的运用.关键是明确立体图形与其平面展开图形之间的数量关系,充分运用勾股定理及三角函数的定义解题.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:选择题
| 每天使用零花钱(单位:元) | 1 | 2 | 3 | 4 | 5 |
| 人数 | 1 | 3 | 6 | 5 | 5 |
| A. | 3,3 | B. | 3,3.5 | C. | 3.5,3.5 | D. | 3.5,3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 878.97×108元 | B. | 878.97×109元 | C. | 8.7897×1010元 | D. | 8.7897×1011元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{5}{3}$ | B. | $\frac{5}{3}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
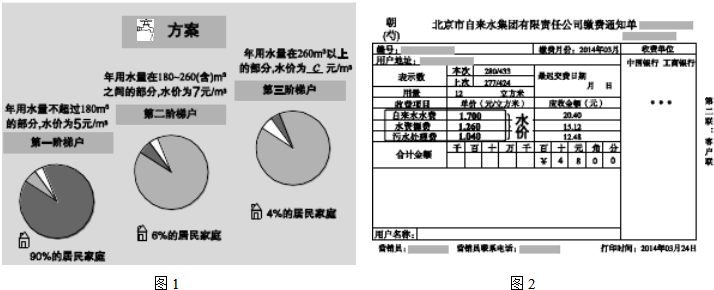
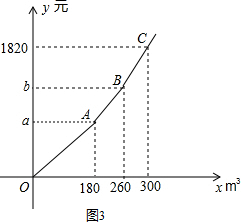
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com