
【题目】网上办公,手机上网已成为人们日常生活的一部分,我县某通信公司为普及网络使用,特推出以下两种电话拨号上网收费方式,用户可以任选其一.
收费方式一(计时制):0.05元/分;
收费方式二(包月制):50元/月(仅限一部个人电话上网);
同时,每一种收费方式均对上网时间加收0.02元/分的通信费.
某用户一周内的上网时间记录如下表:
日期 | 上网时间(分钟) |
星期一 | 35 |
星期二 | 40 |
星期三 | 33 |
星期四 | 50 |
星期五 | 34 |
星期六 | 40 |
星期日 | 48 |
(1)计算该用户一周内平均每天上网的时间.
(2)设该用户12月份上网的时间为![]() 小时,请你分别写出两种收费方式下该用户所支付的费用. (用含
小时,请你分别写出两种收费方式下该用户所支付的费用. (用含![]() 的代数式表示)
的代数式表示)
(3)如果该用户在一个月(30天)内,按(1)中的平均每天上网时间计算,你认为采用哪种方式支付费用较为合算?并说明理由.
【答案】(1) ![]() h;(2) (2)方式一的费用为:0.05×60x+0.02×60x=4.2x(元);方式二的费用为:50+0.02×60x=(50+1.2x)(元);(3) 包月制合算.
h;(2) (2)方式一的费用为:0.05×60x+0.02×60x=4.2x(元);方式二的费用为:50+0.02×60x=(50+1.2x)(元);(3) 包月制合算.
【解析】
(1)平均时间=![]() ;
;
(2)第一种是费用=每分钟的费用×时间+通信费,第二种的费用=月费+通信费
(3)将30乘(1)计算出的平均时间,得到费用的大小,再进行比较就可以得出结论
解:(1)该用户一周内平均每天上网的时间
![]() =40(分钟)=
=40(分钟)=![]() h
h
答:该用户一周内平均每天上网的时间是![]() h;
h;
(2)采用收费方式一(计时制)的费用为:0.05×60x+0.02×60x=4.2x(元)
采用收费方式二(包月制)的费用为:50+0.02×60x=(50+1.2x)(元);
(3)若一个月内上网的时间为30x=20小时
则计时制应付的费用为4.2×20=84(元),包月制应付的费用为50+1.2×20=74(元).
由84 > 74,所以包月制合算.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)画出△ABC关于点B成中心对称的图形△A1BC1;
(2)以原点O为位似中心,相似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出点C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
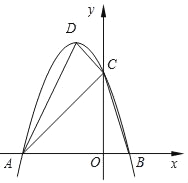
【题目】如图,已知在平面直角坐标系xOy中,抛物线y=ax2﹣2x+c与x轴交于点A和点B(1,0),与y轴相交于点C(0,3).
(1)求抛物线的解析式和顶点D的坐标;
(2)求证:∠DAB=∠ACB;
(3)点Q在抛物线上,且△ADQ是以AD为底的等腰三角形,求Q点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织学生春游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满,已知45座客车每日每辆租金为220元,60座客车每日每辆租金为300元.试问:
(1)春游学生共多少人,原计划租45座客车多少辆?
(2)若租用同一种车,要使每位同学都有座位,怎样租车更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列等式:①由a=b,得5﹣2a=5﹣2b;②由a=b,得ac=bc;③由a=b,得![]() ;④由
;④由![]() ,得3a=2b;
,得3a=2b;
⑤由a2=b2,得a=b.其中正确的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于![]() AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )

A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,…,第n次移动到An.则△OA2A2018的面积是( )

A. 504m2 B. ![]() m2 C.
m2 C. ![]() m2 D. 1009m2
m2 D. 1009m2
查看答案和解析>>
科目:初中数学 来源: 题型:
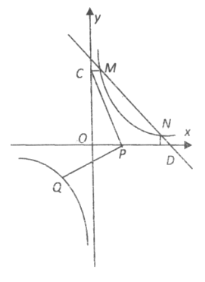
【题目】已知:如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于M,N两点,过点M作MC⊥y轴于点C,且CM=1,过点N作ND⊥x轴于点D,且DN=1,已知点P是x轴(除原点O外)上一点.
的图象交于M,N两点,过点M作MC⊥y轴于点C,且CM=1,过点N作ND⊥x轴于点D,且DN=1,已知点P是x轴(除原点O外)上一点.
(1)直接写出M、N的坐标及k的值;
(2)将线段CP绕点P按逆时针旋转90°得到线段PQ,当点P滑动时,点Q能否在反比例函数的图象上?如果能,求出点Q的坐标;如果不能,请说明理由;
(3)当点P滑动时,是否存在反比例函数图象(第一象限的一支)上的点S,使得以P、S、M、N四个点为顶点的四边形是平行四边形?若存在,请直接写出所有符合题意的点S的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com