
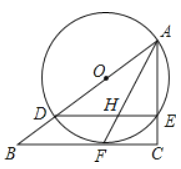
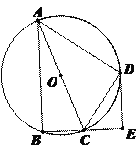
【题目】如图,在Rt△ABC中,∠C=90°,点D是AB上一点,以AD为直径作⊙O交AC于E,与BC相切于点F,连接AF.
(1)求证:∠BAF=∠CAF;
(2)若AC=6,BC=8,求BD和CE的长;
(3)在(2)的条件下,若AF与DE交于H,求FHFA的值.(直接写出结果即可)
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)连结OF,如图,根据切线的性质得OF⊥BC,则易得OF∥AC,所以∠OFA=∠CAF,加上∠OAF=∠OFA,则∠BAF=∠CAF;
(2)设⊙O的半径为r,OF与DE交于点P,如图,在Rt△ABC中根据勾股定理计算出AB=10,再证明△BOF∽△BAC,利用相似比计算出r=![]() ,则BD=BA-AD=
,则BD=BA-AD=![]() ;接着根据圆周角定理由AD为⊙O的直径得到∠AED=90°,易得DE∥BC,根据平行线分线段成比例定理可计算出CE=
;接着根据圆周角定理由AD为⊙O的直径得到∠AED=90°,易得DE∥BC,根据平行线分线段成比例定理可计算出CE=![]() ;
;
(3)根据平行线分线段成比例定理,由OF∥AC,![]() ,则可计算出CF=3,再在Rt△ACF中,利用勾股定理计算出AF=3
,则可计算出CF=3,再在Rt△ACF中,利用勾股定理计算出AF=3![]() ,然后利用HE∥CF得到
,然后利用HE∥CF得到![]() ,可计算出FH=
,可计算出FH=![]() ,最后计算FHFA的值.
,最后计算FHFA的值.
解答:(1)证明:连结OF,如图,
∵⊙O与BC相切于点F,
∴OF⊥BC,
∵∠ACB=90°,
∴OF∥AC,
∴∠OFA=∠CAF,
而OA=OF,
∴∠OAF=∠OFA,
∴∠BAF=∠CAF;
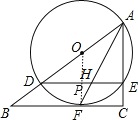
(2)解:设⊙O的半径为r,OF与DE交于点P,如图,
在Rt△ABC中,∵AC=6,BC=8,
∴AB=![]() =10,
=10,
∵OF∥AC,
∴△BOF∽△BAC,
∴![]() =
=![]() ,即
,即
![]() =
=![]() ,解得r=
,解得r=![]() ,
,
∴BD=BA-AD=10-2×![]() =
=![]() ,
,
∵AD为⊙O的直径,
∴∠AED=90°,
而∠C=90°,
∴DE∥BC,
∴![]() =
=![]() ,即
,即
![]() =
=![]() ,
,
∴CE=![]() ;
;
(3)解:∵OF∥AC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得CF=3,
,解得CF=3,
在Rt△ACF中,AF=![]() =3
=3![]() ,
,
∵HE∥CF,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴FH=![]() ,
,
∴FHFA=![]() 3
3![]() =
=![]() .
.


科目:初中数学 来源: 题型:
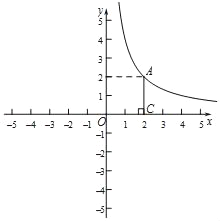
【题目】如图,在平面直角坐标系xOy中,函数y=![]() (x>0)的图象经过点A,作AC⊥x轴于点C.
(x>0)的图象经过点A,作AC⊥x轴于点C.
(1)求k的值;
(2)直线y=ax+b(a≠0)图象经过点A交x轴于点B,且OB=2AC.求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
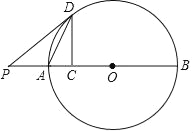
【题目】如图,点C是⊙O直径AB上一点,过C作CD⊥AB交⊙O于点D,连接DA,延长BA至点P,连接DP,使∠PDA=∠ADC.
(1)求证:PD是⊙O的切线;
(2)若AC=3,tan∠PDC=![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形, ![]() ,AC为直径, DE⊥BC,垂足为E.
,AC为直径, DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
(2)若AC=9,CE=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
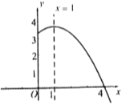
【题目】抛物线![]() 的部分图像如图所示,抛物线的对称轴是直线
的部分图像如图所示,抛物线的对称轴是直线![]() ,与
,与![]() 轴的一个交点坐标为(4,0).下列结论中:①
轴的一个交点坐标为(4,0).下列结论中:①![]() ;②
;②![]() ;③方程
;③方程![]() 有两个不相等的实数根;④抛物线与
有两个不相等的实数根;④抛物线与![]() 轴的另一个交点坐标为(–1,0);⑤若点
轴的另一个交点坐标为(–1,0);⑤若点![]() 在该抛物线上,则
在该抛物线上,则![]() .其中正确的有( )
.其中正确的有( )
A. ①③④ B. ②③④ C. ①③⑤ D. ①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A,C分别在x轴、y轴的正半轴上,抛物线y=-![]() x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
(1)求此抛物线的解析式;
(2)求此抛物线顶点D的坐标和四边形ABDC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由8个大小相同的小正方体组合成的简单几何体.
(1)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图;(边框线加粗画出,并涂上阴影)

(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和主视图不变,那么请在下列网格图中画出添加小正方体后所得几何体所有可能的左视图.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2;
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2;
(1)求反比例函数的表达式;
(2)根据图象直接写出﹣![]() x>
x>![]() 的解集;
的解集;
(3)将直线l1:y=- ![]() x沿y向上平移后的直线l2与反比例函数y=
x沿y向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
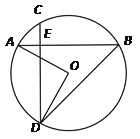
【题目】如图,在⊙O中,弦AB=弦CD,AB⊥CD于点E,且AE<EB,CE<ED,连结AO,DO,BD.
(1)求证:EB=ED.
(2)若AO=6,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com