
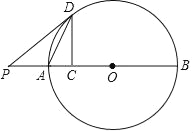
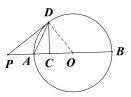
【题目】如图,点C是⊙O直径AB上一点,过C作CD⊥AB交⊙O于点D,连接DA,延长BA至点P,连接DP,使∠PDA=∠ADC.
(1)求证:PD是⊙O的切线;
(2)若AC=3,tan∠PDC=![]() ,求BC的长.
,求BC的长.
【答案】(1)证明见解析;(2)BC=12.
【解析】
(1)求出∠ODA+∠PDA=∠ADC+∠DAO=90°,根据切线的判定得出即可;
(2)求出∠PDC=∠DOC,解直角三角形求出![]() =
=![]() ,设DC=4x,OC=3x,求出3x+3=5x,求出x,即可得出答案.
,设DC=4x,OC=3x,求出3x+3=5x,求出x,即可得出答案.
(1)证明:连接OD
∵OD=OA
∴∠ODA=∠OAD
∵CD⊥AB于点C
∴∠OAD+∠ADC=90°
∴∠ODA+∠ADC= 90°
∵∠PDA=∠ADC
∴∠PDA+∠ODA=90°
即∠PDO=90°
∴PD⊥OD
∵D在⊙O上
∴PD是⊙O的切线
(2)解:∵∠PDO=90°
∴∠PDC+∠CDO=90°
∵CD⊥AB于点C
∴∠DOC+∠CDO=90°
∴∠PDC=∠DOC
![]()
![]() =
=![]()
设DC = 4x,CO = 3x,则OD=5x
∵AC=3
∴OA=3x+3
∴3x+3=5x
∴x=![]()
∴OC=3x=![]() , OD=OB=5x=
, OD=OB=5x=![]()
∴BC=12


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件
B.甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是![]() ,
,![]() ,则甲的射击成绩较稳定
,则甲的射击成绩较稳定
C.“明天降雨的概率为![]() ”,表示明天有半天都在降雨
”,表示明天有半天都在降雨
D.了解一批电视机的使用寿命,适合用普查的方式
查看答案和解析>>
科目:初中数学 来源: 题型:
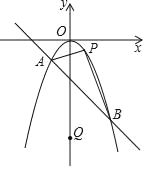
【题目】如图所示,已知抛物线y=ax2(a≠0)与一次函数y=kx+b的图象相交于A(﹣1,﹣1),B(2,﹣4)两点,点P是抛物线上不与A,B重合的一个动点,点Q是y轴上的一个动点.
(1)请直接写出a,k,b的值及关于x的不等式ax2<kx﹣2的解集;
(2)当点P在直线AB上方时,请求出△PAB面积的最大值并求出此时点P的坐标;
(3)是否存在以P,Q,A,B为顶点的四边形是平行四边形?若存在,请直接写出P,Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
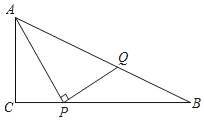
【题目】如图,Rt△ABC中,∠C=90°,P是CB边上一动点,连接AP,作PQ⊥AP交AB于Q.已知AC=3cm,BC=6cm,设PC的长度为xcm,BQ的长度为ycm.
小青同学根据学习函数的经验对函数y随自变量x的变化而变化的规律进行了探究.
下面是小青同学的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y的几组对应值;
x/cm | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 6 |
y/cm | 0 | 1.56 | 2.24 | 2.51 | m | 2.45 | 2.24 | 1.96 | 1.63 | 1.26 | 0.86 | 0 |
(说明:补全表格时,相关数据保留一位小数)
m的值约为多少cm;
(2)在平面直角坐标系中,描出以补全后的表格中各组数值所对应的点(x,y),画出该函数的图象;
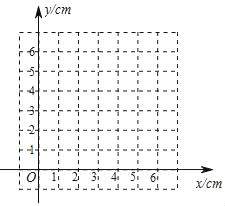
(3)结合画出的函数图象,解决问题:
①当y>2时,写出对应的x的取值范围;
②若点P不与B,C两点重合,是否存在点P,使得BQ=BP?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C是⊙O上的三个点,点D在BC的延长线上.有如下四个结论:①在∠ABC所对的弧上存在一点E,使得∠BCE=∠DCE;②在∠ABC所对的弧上存在一点E,使得∠BAE=∠AEC;③在∠ABC所对的弧上存在一点E,使得EO平分∠AEC;④在∠ABC所对的弧上任意取一点E(不与点A,C重合) ,∠DCE=∠ABO +∠AEO均成立.上述结论中,所有正确结论的序号是( )

A. ①②③ B. ①③④ C. ②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O′在第一象限,⊙O′与x轴相切于H点,与y轴相交于A(0,2),B(0,8),则点O′的坐标是( )

A. (6,4) B. (4,6) C. (5,4) D. (4,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
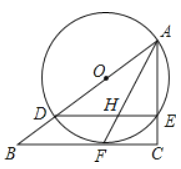
【题目】如图,在Rt△ABC中,∠C=90°,点D是AB上一点,以AD为直径作⊙O交AC于E,与BC相切于点F,连接AF.
(1)求证:∠BAF=∠CAF;
(2)若AC=6,BC=8,求BD和CE的长;
(3)在(2)的条件下,若AF与DE交于H,求FHFA的值.(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市某幼儿园六一期间举行亲子游戏,主持人请三位家长分别带自己的孩子参加游戏,主持人准备把家长和孩子重新组合完成游戏,A、B、C分别表示三位家长,他们的孩子分别对应的是a、b、c.
(1)若主持人分别从三位家长和三位孩子中各选一人参加游戏,恰好是A、a的概率是多少(直接写出答案)
(2)若主持人先从三位家长中任选两人为一组,再从孩子中任选两人为一组,四人共同参加游戏,恰好是两对家庭成员的概率是多少.(画出树状图或列表)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com