练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知三角形三边长分别为2，x，13，若x为整数，则这样的三角形个数为（   ）

    A．2            B．3              C．5            D．13


    B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，在矩形ABCD中，AD=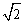AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，有下列结论：①∠AED=∠CED：

        ②OE=OD；③BH=HF，④BC－CF=2HE：⑤AB=HF其中正确的有

        A．2个      B．3个          C．4个              D．5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


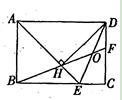
    如图，在Rt△ABC中，∠ACB=90，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD，BE

    （1）    求证：CE=AD

    （2）    当点D在AB中点使，四边形BECD是什么特殊四边形？说明理由

    （3）    若D为AB的中点，则当∠A的大小满足什么条件时，四边形BECD是正方形？说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知抛物线经过点（0，－3），请你确定一个的值，使该抛物线与 轴的一个交点在(1，0)和(3，0)之间，你所确定的的值是         ．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某乒乓球馆使用发球机进行辅助训练，出球口在桌面中线端点A处的正上方，假设每次发出的乒乓球的运动路线固定不变，且落在中线上，在乒乓球运行时，设乒乓球与端点A的水平距离为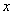（米），与桌面的高度为（米），运行时间为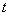（秒），经多次测试后，得到如下部分数据：

    （秒）

    0

    0.16

    0.2

    0.4

    0.6

    0.64

    0.8

    …

    （米）

    0

    0.4

    0.5

    1

    1.5

    1.6

    2

    …

    （米）

    0.25

    0.378

    0.4

    0.45

    0.4

    0.378

    0.25

    …

    （1）当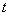为何值时，乒乓球达到最大高度？

    （2）乒乓球落在桌面时，与端点A的水平距离是多少？

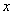    （3）乒乓球落在桌面上弹起后，与满足.

    ①用含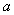的代数式表示；

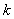    ②球网高度为0.14米，球桌长（1.4×2）米，若球弹起后，恰好有唯一的击球点，可以将球沿直线扣杀到点A，求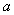的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如果一个多边形的内角和是1 440°，那么这个多边形的边数是_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一机器人以0.2m/s的速度在平地上按下图中的步骤行走，那么该机器人从开始到停止所需时间为    s．

     


                                                                                               

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列计算正确的是(　　)

    A.   B.      C. (a≠0)     D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：x2•x5=____ ______

    查看答案和解析>>

    同步练习册答案