
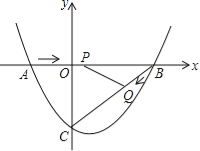
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣2,0)、B(4,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK:S△PBQ=5:2,求K点坐标.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣3
x﹣3
(2)运动1秒使△PBQ的面积最大,最大面积是![]()
(3)K1(1,﹣![]() ),K2(3,﹣
),K2(3,﹣![]() )
)
【解析】
试题(1)把点A、B的坐标分别代入抛物线解析式,列出关于系数a、b的解析式,通过解方程组求得它们的值;
(2)设运动时间为t秒.利用三角形的面积公式列出S△PBQ与t的函数关系式S△PBQ=﹣![]() (t﹣1)2+
(t﹣1)2+![]() .利用二次函数的图象性质进行解答;
.利用二次函数的图象性质进行解答;
(3)利用待定系数法求得直线BC的解析式为y=![]() x﹣3.由二次函数图象上点的坐标特征可设点K的坐标为(m,
x﹣3.由二次函数图象上点的坐标特征可设点K的坐标为(m,![]() m2﹣
m2﹣![]() m﹣3).
m﹣3).
如图2,过点K作KE∥y轴,交BC于点E.结合已知条件和(2)中的结果求得S△CBK=![]() .则根据图形得到:S△CBK=S△CEK+S△BEK=
.则根据图形得到:S△CBK=S△CEK+S△BEK=![]() EKm+
EKm+![]() EK(4﹣m),把相关线段的长度代入推知:﹣
EK(4﹣m),把相关线段的长度代入推知:﹣![]() m2+3m=
m2+3m=![]() .易求得K1(1,﹣
.易求得K1(1,﹣![]() ),K2(3,﹣
),K2(3,﹣![]() ).
).
解:(1)把点A(﹣2,0)、B(4,0)分别代入y=ax2+bx﹣3(a≠0),得
![]() ,
,
解得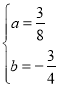 ,
,
所以该抛物线的解析式为:y=![]() x2﹣
x2﹣![]() x﹣3;
x﹣3;
(2)设运动时间为t秒,则AP=3t,BQ=t.
∴PB=6﹣3t.
由题意得,点C的坐标为(0,﹣3).
在Rt△BOC中,BC=![]() =5.
=5.
如图1,过点Q作QH⊥AB于点H.
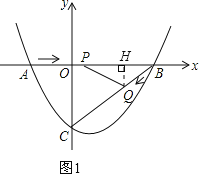
∴QH∥CO,
∴△BHQ∽△BOC,
∴![]()
![]() ,即
,即![]()
![]() ,
,
∴HQ=![]() t.
t.
∴S△PBQ=![]() PBHQ=
PBHQ=![]() (6﹣3t)
(6﹣3t)![]() t=﹣
t=﹣![]() t2+
t2+![]() t=﹣
t=﹣![]() (t﹣1)2+
(t﹣1)2+![]() .
.
当△PBQ存在时,0<t<2
∴当t=1时,
S△PBQ最大=![]() .
.
答:运动1秒使△PBQ的面积最大,最大面积是![]() ;
;
(3)设直线BC的解析式为y=kx+c(k≠0).
把B(4,0),C(0,﹣3)代入,得
![]() ,
,
解得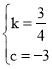 ,
,
∴直线BC的解析式为y=![]() x﹣3.
x﹣3.
∵点K在抛物线上.
∴设点K的坐为(m,![]() m2﹣
m2﹣![]() m﹣3).
m﹣3).
如图2,过点K作KE∥y轴,交BC于点E.则点E的坐标为(m,![]() m﹣3).
m﹣3).
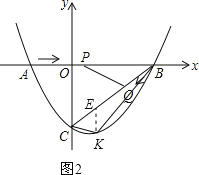
∴EK=![]() m﹣3﹣(
m﹣3﹣(![]() m2﹣
m2﹣![]() m﹣3)=﹣
m﹣3)=﹣![]() m2+
m2+![]() m.
m.
当△PBQ的面积最大时,∵S△CBK:S△PBQ=5:2,S△PBQ=![]() .
.
∴S△CBK=![]() .
.
S△CBK=S△CEK+S△BEK=![]() EKm+
EKm+![]() EK(4﹣m)
EK(4﹣m)
=![]() ×4EK
×4EK
=2(﹣![]() m2+
m2+![]() m)
m)
=﹣![]() m2+3m.
m2+3m.
即:﹣![]() m2+3m=
m2+3m=![]() .
.
解得 m1=1,m2=3.
∴K1(1,﹣![]() ),K2(3,﹣
),K2(3,﹣![]() ).
).


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】一个四位数,记千位数字与个位数字之和为![]() ,十位数字与百位数字之和为
,十位数字与百位数字之和为![]() ,如果
,如果![]() ,那么称这个四位数为“对称数”
,那么称这个四位数为“对称数”
![]() 最小的“对称数”为 ;四位数
最小的“对称数”为 ;四位数![]() 与
与![]() 之和为最大的“对称数”,则
之和为最大的“对称数”,则![]() 的值为 ;
的值为 ;
![]() 一个四位的“对称数”
一个四位的“对称数”![]() ,它的百位数字是千位数字
,它的百位数字是千位数字![]() 的
的![]() 倍,个位数字与十位数字之和为
倍,个位数字与十位数字之和为![]() ,且千位数字
,且千位数字![]() 使得不等式组
使得不等式组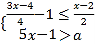 恰有
恰有![]() 个整数解,求出所有满足条件的“对称数”
个整数解,求出所有满足条件的“对称数”![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知半圆⊙O的直径AB=10,弦CD∥AB,且CD=8,E为弧CD的中点,点P在弦CD上,联结PE,过点E作PE的垂线交弦CD于点G,交射线OB于点F.
(1)当点F与点B重合时,求CP的长;
(2)设CP=x,OF=y,求y与x的函数关系式及定义域;
(3)如果GP=GF,求△EPF的面积.
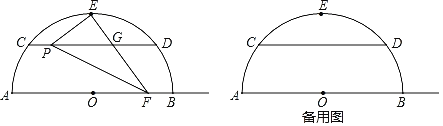
查看答案和解析>>
科目:初中数学 来源: 题型:
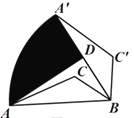
【题目】如图,在△ABC中,AB=4,若将△ABC绕点B顺时针旋转60°,点A的对应点为点A′,点C的对应点为点C′,点D为A′B的中点,连接AD.则点A的运动路径![]() 与线段AD、A′D围成的阴影部分面积是______.
与线段AD、A′D围成的阴影部分面积是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
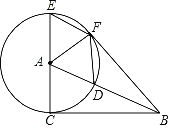
【题目】如图,在![]() ABC中,∠ACB=90°,以点A为圆心,AC的长为半径作⊙A,交AB于点D,交CA的延长线于点E.过点E作EF∥AB,交⊙A于点F,连接AF,BF,DF.
ABC中,∠ACB=90°,以点A为圆心,AC的长为半径作⊙A,交AB于点D,交CA的延长线于点E.过点E作EF∥AB,交⊙A于点F,连接AF,BF,DF.
(1)求证:BF是⊙A的切线;
(2)填空:
①当四边形ADFE是周长为20的菱形时,BF= ;
②当![]() = 时,四边形ACBF是正方形.
= 时,四边形ACBF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把如图1所示的菱形称为基本图形,将此基本图形不断复制并平移,使得相邻两个基本图形的一个顶点与对称中心重合,得到的所有菱形都称为基本图形的特征图形,显然图2中有3个特征图形.

(1)观察以上图形并完成如表:
根据表中规律猜想,图n(n≥2)中特征图形的个数为 .(用含n的式子表示)
图形名称 | 基本图形的个数 | 特征图形的个数 |
图1 | 1 | 1 |
图2 | 2 | 3 |
图3 | 3 | 7 |
图4 | 4 | |
…… | …… | …… |
(2)若基本图形的面积为2,则图2中小特征图形的面积是 ;图2020中所有特征图形的面积之和为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
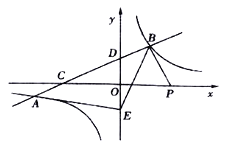
【题目】如图,直线![]() 与双曲线
与双曲线![]() 交于点
交于点![]() 和点
和点![]() ,与
,与![]() 轴、
轴、![]() 轴的交点分别为点
轴的交点分别为点![]() ,点
,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 是
是![]() 轴上一个动点.
轴上一个动点.
(1)填空:①![]() ,
,![]() ;
;
②B点的坐标是 .
(2)若![]() ,求此时点
,求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com