
���� ��1�����ݵ�x=-1��x=3ʱ�����κ�����ֵy��ȣ�����Գ��ᣬ�ɵ�A������Ϊ��-2��0�����õ�B������Ϊ��4��0������A��-2��0����B��4��0���ֱ�������ʽy=ax2+bx-4���ɣ�
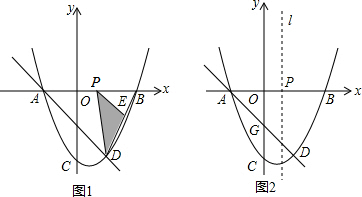
��2����ͼ1����EF��x����F�����AD����ʽ���ɵõ�PE����ʽΪy=-x+g����E��t��2t-8������E��t��2t-8������y=-x+g��2t-8=-t+g����g=3t-8��PE����ʽΪy=-x+3t-8�����P������Ϊ��3t-8��0�����г�S��DPE=[4-��3t-8��][4-8+2t]=-6t2+36t-48������⣻
��3�����κ����Գ���Ϊx=1����C��0��-4������x=1�ĶԳƵ�ΪC�䣨2��-4����G��0��-2������x��ĶԳƵ�ΪG�䣨0��2��������C��G�䣬��l���㼴ΪM����x�ύ�㼴ΪN����ʱ�ı���CMNG���ܳ���Сֵ=C��G�䣮���C��G�����ʽ���ɽ��
��� �⣺��1����x=-1��x=3ʱ�����κ�����ֵy��ȿ�֪�Գ���Ϊx=$\frac{-1+3}{2}$=1��
�ߵ�A������Ϊ��-2��0����
��B��������4��0����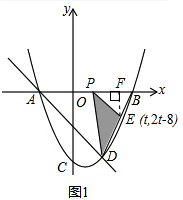
��A��-2��0����B��4��0���ֱ�������ʽ�ã�
$\left\{\begin{array}{l}4a-2b-4=0\\ 16a+4b-4=0\end{array}\right.$��
���$\left\{\begin{array}{l}a=\frac{1}{2}\\ b=-1\end{array}\right.$��
���κ�������ʽΪy=$\frac{1}{2}$x2-x-4��
��2����ͼ1����EF��x����F������D��2��m������y=$\frac{1}{2}$x2-x-4�ã�m=-4��
��D��������2��-4����
��AD����ʽΪy=kx+b��
��A��-2��0����D��2��-4���ֱ�������ʽ�ã�$\left\{\begin{array}{l}-2k+b=0\\ 2k+b=-4\end{array}\right.$����ã�$\left\{\begin{array}{l}b=-2\\ k=-1\end{array}\right.$��
����AD����ʽΪy=-x-2��
��PE��AD��
��PE����ʽΪy=-x+g��
��BD����ʽΪy=mx+n��
��B��4��0����D��2��-4���ֱ�������ʽ�ã�$\left\{\begin{array}{l}4m+n=0\\ 2m+n=-4\end{array}\right.$����ã�$\left\{\begin{array}{l}m=2\\ n=-8\end{array}\right.$��
����BD����ʽΪy=2x-8��
�����E��t��2t-8������E��t��2t-8������y=-x+g��2t-8=-t+g����g=3t-8��
PE����ʽΪy=-x+3t-8��
��y=0ʱ��x=3t-8����P������Ϊ��3t-8��0����
S��DPE=[4-��3t-8��][4-8+2t]=-6t2+36t-48��
��t=-$\frac{36}{2����-6��}$=3ʱ��S��DPE��������
��ʱ��3t-8=3��3-8=1��
��P��1��0����
��3����ͼ2�����κ����Գ���Ϊx=1����C��0��-4������x=1�ĶԳƵ�ΪC�䣨2��-4����G��0��-2������x��ĶԳƵ�ΪG�䣨0��2����
����C��G�䣬��l���㼴ΪM����x�ύ�㼴ΪN��
��ʱ�ı���CMNG���ܳ���Сֵ=C��G�䣮
��C��G��Ľ���ʽΪy=zx+s��
��C�䣨2��-4����G�䣨0��2���ֱ�������ʽ�ã�$\left\{\begin{array}{l}2z+s=-4\\ s=2\end{array}\right.$��
��ã�$\left\{\begin{array}{l}z=-3\\ s=2\end{array}\right.$��
C��G��Ľ���ʽΪy=-3x+2��
��x=1ʱ��y=-1��M��1��-1����
��y=0ʱ��x=$\frac{2}{3}$��N��$\frac{2}{3}$��0����
�ı���CMNG���ܳ���Сֵ=C��G��+CG=$\sqrt{��0-2��^{2}+��2+4��^{2}}$+2=2$\sqrt{10}$+2��
���� ���⿼���˶��κ����ۺ��⣬�漰����ϵ������һ�κ�������ʽ�����κ�������ʽ�����κ�������ֵ����Գ����·�����⣬�ѶȽϴ�ֵ�ù�ע��


 ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д�
ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д� â���̸����������������ϵ�д�
â���̸����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
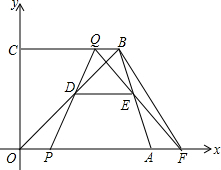 ��ͼ����ֱ������OABC�У�OA��CB��A��B���������ֱ�ΪA��15��0����B��10��12��������P��Q�ֱ��O��B��������P��ÿ��2����λ���ȵ��ٶ���OA���յ�A�˶�����Q��ÿ��1����λ���ٶ���BC���յ�C�˶�������Pֹͣ�˶�ʱ����QҲͬʱֹͣ�˶����߶�OB��PQ�ཻ�ڵ�D������D��DE��OA����AB�ڵ�E������QE���ӳ�����x���ڵ�F���趯��P��Q���˶�ʱ��Ϊt����λ���룩
��ͼ����ֱ������OABC�У�OA��CB��A��B���������ֱ�ΪA��15��0����B��10��12��������P��Q�ֱ��O��B��������P��ÿ��2����λ���ȵ��ٶ���OA���յ�A�˶�����Q��ÿ��1����λ���ٶ���BC���յ�C�˶�������Pֹͣ�˶�ʱ����QҲͬʱֹͣ�˶����߶�OB��PQ�ཻ�ڵ�D������D��DE��OA����AB�ڵ�E������QE���ӳ�����x���ڵ�F���趯��P��Q���˶�ʱ��Ϊt����λ���룩�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
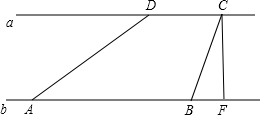 ��ͼ����������a��bƽ�У�C��D�ǺӰ�a�ϼ��50���������߸ˣ�ij���ںӰ�b�ϵ�A����á�DAE=30�㣬Ȼ���غӰ�����100����B������á�CBF=60�㣬������Ŀ���CF��ֵΪ43m�������ȷ����λ��$\sqrt{2}$��1.414��$\sqrt{3}$��1.732��
��ͼ����������a��bƽ�У�C��D�ǺӰ�a�ϼ��50���������߸ˣ�ij���ںӰ�b�ϵ�A����á�DAE=30�㣬Ȼ���غӰ�����100����B������á�CBF=60�㣬������Ŀ���CF��ֵΪ43m�������ȷ����λ��$\sqrt{2}$��1.414��$\sqrt{3}$��1.732���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
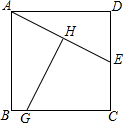 ��ͼ��E��������ABCD�ı�CD���е㣬AE�Ĵ�ֱƽ���߷ֱ�AE��BC��H��G����CG=7����������ABCD���������64��
��ͼ��E��������ABCD�ı�CD���е㣬AE�Ĵ�ֱƽ���߷ֱ�AE��BC��H��G����CG=7����������ABCD���������64���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
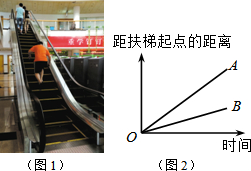 ���������������е��Զ�����������ȥ��¥����ͼ1����ͼ2���߶�OA��OB�ֱ��ʾ�����������е��Զ�����������ȥ��¥�;�ֹվ�������е��Զ�������ȥ��¥ʱ�����Զ��������ľ�����ʱ��֮��Ĺ�ϵ�������ĸ�ͼ�У�����OC�ܴ��±�ʾ������ֹͣ���У�����ֹ�����Զ�����������ȥ��¥ʱ�����Զ��������ľ�����ʱ���ϵ���ǣ�������
���������������е��Զ�����������ȥ��¥����ͼ1����ͼ2���߶�OA��OB�ֱ��ʾ�����������е��Զ�����������ȥ��¥�;�ֹվ�������е��Զ�������ȥ��¥ʱ�����Զ��������ľ�����ʱ��֮��Ĺ�ϵ�������ĸ�ͼ�У�����OC�ܴ��±�ʾ������ֹͣ���У�����ֹ�����Զ�����������ȥ��¥ʱ�����Զ��������ľ�����ʱ���ϵ���ǣ�������| A�� | 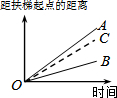 | B�� | 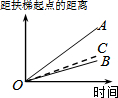 | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com