练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．某过天桥的设计图是梯形ABCD（如图所示），桥面DC与地面AB平行，DC=62米，AB=88米．左斜面AD与地面AB的夹角为23°，右斜面BC与地面AB的夹角为30°，立柱DE⊥AB于E，立柱CF⊥AB于F，求桥面DC与地面AB之间的距离（精确到0.1米）sin23°=0.3907，cos23°=0.9205，tan23°=0.4245

    分析 首先设桥面DC与地面AB之间的距离为x米，分别用x表示出AE和BF，AE+BF=AB-DC，则得到关于x的一元一次方程，从而求出x．

    解答 解：设桥面DC与地面AB之间的距离为x米，即DE=CF=xm，
    则AE=$\frac{x}{tan23°}$，BF=$\frac{x}{tan30°}$，
    AE+BF=AB-DC，
    则$\frac{x}{tan23°}$+$\frac{x}{tan30°}$=88-62，
    解得：x≈6.4．
    答：桥面DC与地面AB之间的距离约为6.4米．

    点评 此题考查的是解直角三角形的应用-坡度坡角问题．关键是由两个直角三角形得出关于桥面DC与地面AB之间的距离的方程求解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    3．设$6-\sqrt{13}$的整数部分为a，小数部分为b，那么2a-b的值是（　　）
    A．$3-\sqrt{3}$B．$4-\sqrt{13}$C．$\sqrt{13}$D．$4+\sqrt{13}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．现将长为3cm的线段AB向右平移6cm得到线段A′B′，则点B与点B′之间的距离为（　　）
    A．0cmB．3cmC．6cmD．9cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．下列计算中，正确的是（　　）
    A．-2（a-b）=-2a-2bB．$\sqrt{5}-\sqrt{2}=\sqrt{3}$C．$\frac{-x+y}{x-y}=-1$D．（2a2b）2=2a4b2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．先化简，再求值：$（{x-2+\frac{3}{x+2}}）÷\frac{{{x^2}+2x+1}}{x+2}$，其中x=-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．下列手机屏幕上显示的图标是轴对称图形的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

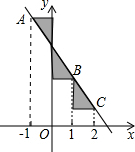    5．如图，点A、B、C在一次函数y=-2x+m的图象上，它们的横坐标依次为-1，1，2，分别过这些点作x轴与y轴的垂线，则图中阴影部分的面积之和是（　　）
    A．3（m-1）B．$\frac{3}{2}（m-2）$C．1D．3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．解下列方程组：
    （1）$\left\{\begin{array}{l}{5x+2y=8}\\{3x-y=7}\end{array}\right.$（用代入法）
    （2）$\left\{\begin{array}{l}{3x-2y=8}\\{x+2y=16}\end{array}\right.$（用加减法）
    （3）$\left\{\begin{array}{l}{x-2=2（y-1）}\\{2（x-2）+（y-1）=5}\end{array}\right.$
    （4）$\left\{\begin{array}{l}{\frac{x+1}{3}=\frac{y+2}{4}}\\{\frac{x-3}{4}-\frac{y-3}{3}=\frac{1}{12}}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．计算：（$\frac{1}{2}$）-2-（π-3.14）0-|-$\root{3}{8}$|+2cos60°．

    查看答案和解析>>

    同步练习册答案