
°æƒø°ø2018ƒÍ∆Ω≤˝∂¨∞¬ª·‘⁄2‘¬9»’µΩ25»’‘⁄∫´π˙∆Ω≤˝ø§æŸ––°£Œ™¡Àµ˜≤È÷–—ß…˙∂‘∂¨∞¬ª·±»»¸œÓƒøµƒ¡ÀΩ‚≥Ã∂»£¨ƒ≥÷–—ß‘⁄—ß…˙÷–◊ˆ¡À“ª¥Œ≥È—˘µ˜≤È£¨µ˜≤ÈΩ·π˚π≤∑÷Œ™Àƒ∏ˆµ»º∂£∫A°¢∑«≥£¡ÀΩ‚ B°¢±»Ωœ¡ÀΩ‚ C°¢ª˘±æ¡ÀΩ‚ D°¢≤ª¡ÀΩ‚°£∏˘æðµ˜≤ÈÕ≥º∆Ω·π˚£¨ªÊ÷∆¡À»ÁÕºÀ˘ 浃≤ªÕÍ’˚µƒ»˝÷÷Õ≥º∆Õº±Ì°£
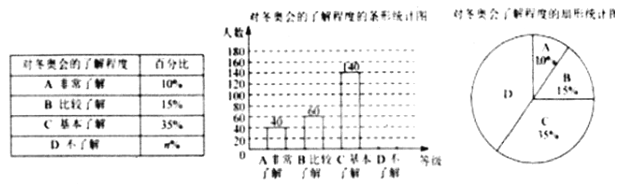
£®1£©±æ¥Œµ˜≤ȵƒ—˘±æ»ð¡ø « £¨n= £ª
£®2£©«Î≤π»´Ãı–ŒÕ≥º∆Õº£ª
£®3£©—ß–£◊º±∏ø™’π∂¨∞¬ª·µƒ÷™ ∂æ∫»¸£¨∏√–£π≤”–4000√˚—ß…˙£¨«Îƒ„π¿º∆’‚À˘—ß–£±æ¥Œæ∫»¸°∞∑«≥£¡ÀΩ‚°±∫Õ°∞±»Ωœ¡ÀΩ‚°±µƒ—ß…˙◊Ð ˝°£
°æ¥∞∏°ø£®1£©400£¨40£ª£®2£©≤πÕºº˚Ω‚Œˆ£ª£®3£©1000
°æΩ‚Œˆ°ø∑÷Œˆ: £®1£©∏˘æðÕ≥º∆Õºø…“‘«Û≥ˆ—˘±æ»ð¡ø∫Õ’‚¥Œµ˜≤ȵƒnµƒ÷µ£ª
£®2£©∏˘æð“‚ø…“‘«Ûµ√µ˜≤ÈŒ™Dµƒ»À ˝£¨¥”∂¯ø…“‘Ω´Ãı–ŒÕ≥º∆Õº≤π≥‰ÕÍ’˚£ª
£®4£©∏˘æð“‚ø…“‘”√—˘±æπ¿º∆◊Ð㨥”∂¯ø…“‘Ω‚¥±æÂ.
œÍΩ‚: £∫£®1£©±æ¥Œµ˜≤ȵƒ—˘±æ»ð¡ø «40°¬10%=400£¨
n%=1-10%-15%-35%=40%£¨
π ¥∞∏Œ™£∫400£¨40£ª
£®2£©µ˜≤ȵƒΩ·π˚Œ™Dµ»º∂µƒ»À ˝Œ™£∫400°¡40%=160£¨
π ≤π»´µƒÃı–ŒÕ≥º∆Õº»ÁÕºÀ˘ 棨
£®4£©”…“‚ø…µ√£¨ 4000°¡£®10%+15%£©=1000£®»À£©
À˘“‘’‚À˘—ß–£±æ¥Œæ∫»¸°∞∑«≥£¡ÀΩ‚°±∫Õ°∞±»Ωœ¡ÀΩ‚°±µƒ—ß…˙◊Ð ˝Œ™1000»À.



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥π´Àæ‘⁄±±≤øÕÂæ≠º√«¯≈©“µ æ∑∂ª˘µÿ≤…π∫A£¨B¡Ω÷÷≈©≤˙∆∑£¨“—÷™A÷÷≈©≤˙∆∑√ø«ßøÀµƒΩ¯º€±»B÷÷∂ý2‘™£¨«“”√24000‘™π∫¬ÚA÷÷≈©≤˙∆∑µƒ ˝¡ø£®∞¥÷ÿ¡øº∆£©”Δ√18000‘™π∫¬ÚB÷÷≈©≤˙∆∑µƒ ˝¡ø£®∞¥÷ÿ¡øº∆£©œýÕ¨£Æ
£®1£©«ÛA£¨B¡Ω÷÷≈©≤˙∆∑√ø«ßøÀµƒΩ¯º€∑÷± «∂ý…Ÿ‘™£ø
£®2£©∏√π´Àæº∆ªÆπ∫Ω¯A£¨B¡Ω÷÷≈©≤˙∆∑π≤40∂÷£¨≤¢‘ÀÕ˘“ϵÿœ˙ €£¨‘À∑—Œ™500‘™/∂÷£¨“—÷™A÷÷≈©≤˙∆∑ €º€Œ™15‘™/kg£¨B÷÷≈©≤˙∆∑ €º€Œ™12‘™/kg£¨∆‰÷–A÷÷≈©≤˙∆∑÷¡…Ÿπ∫Ω¯15∂÷«“≤ª≥¨π˝B÷÷≈©≤˙∆∑µƒ ˝¡ø£¨Œ ∏√π´À收»Á∫Œ≤…π∫≤≈ƒÐªÒµ√◊Ó¥Û¿˚»Û£¨◊Ó¥Û¿˚»Û «∂ý…Ÿ£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
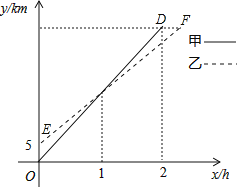
°æƒø°ø‘⁄“ªÃı± ÷±µƒπ´¬∑…œ“¿¥Œ”–A°¢B°¢C»˝µÿ£¨◊‘––≥µ∞Æ∫√’þº◊°¢““¡Ω»À∑÷±¥”A°¢B¡ΩµÿÕ¨ ±≥ˆ∑¢£¨—ÿ÷±œþ‘»ÀŸ∆ÔœÚCµÿ£Æ“—÷™º◊µƒÀŸ∂»Œ™20km/h£¨»ÁÕºÀ˘ 棨º◊°¢““¡Ω»À”ÎAµÿµƒæý¿Îy(km)”Ζ– ª ±º‰x(h)µƒ∫Ø ˝ÕºœÛ∑÷±Œ™œþ∂ŒOD°¢EF£Æ
(1)A°¢B¡Ωµÿµƒæý¿ÎŒ™______km£Æ
(2)«Ûœþ∂ŒEFÀ˘‘⁄÷±œþ∂‘”¶µƒ∫Ø ˝πÿœµ Ω£Æ
(3)»Ù¡Ω»À‘⁄≥ˆ∑¢ ±∂º≈‰±∏¡ÀÕ®ª∞æý¿ÎŒ™3kmµƒ∂‘Ω≤ª˙£¨«Ûº◊°¢““¡Ω»Àæ˘‘⁄∆Ô––π˝≥Ã÷–ø…“‘”√∂‘Ω≤ª˙Õ®ª∞µƒ ±º‰∂Œ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™≈◊ŒÔœþ![]() æ≠π˝
æ≠π˝![]() °¢
°¢![]() ¡Ωµ„.
¡Ωµ„.
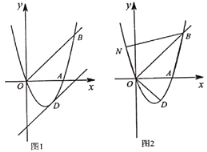
£®1£©«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
£®2£©Ω´÷±œþOBœÚœ¬∆Ω“∆m∏ˆµ•Œª≥§∂»∫Û£¨µ√µΩµƒ÷±œþ”Î≈◊ŒÔœþ÷ª”–“ª∏ˆπ´π≤µ„D£¨«Ûmµƒ÷µº∞µ„Dµƒ◊¯±Í£ª
£®3£©»ÁÕº£¨“—÷™µ„N‘⁄≈◊ŒÔœþ…œ£¨«“![]() .
.
¢Ÿ«Û≥ˆµ„Nµƒ◊¯±Í£ª
¢⁄‘⁄£®2£©µƒÃıº˛œ¬£¨÷±Ω”–¥≥ˆÀ˘”–¬˙◊„![]() µƒµ„Pµƒ◊¯±Í.
µƒµ„Pµƒ◊¯±Í.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥≥¨ –Œ™¡Àœ˙ €“ª÷÷–¬–Õ°∞Œ¸ÀÆÕœ∞—°±£¨∂‘œ˙ €«Èøˆ◊˜¡Àµ˜≤È£¨Ω·π˚∑¢œ÷√ø‘¬œ˙ €¡øy£®÷ª£©”Îœ˙ €µ•º€x£®‘™£©¬˙◊„“ª¥Œ∫Ø ˝πÿœµ£¨À˘µ˜≤ȵƒ≤ø∑÷ ˝æð»Á±Ì£∫£®“—÷™√ø÷ªΩ¯º€Œ™10‘™£¨œ˙ €µ•º€Œ™’˚ ˝£¨√ø÷ª¿˚»Û£Ωœ˙ €µ•º€©ÅΩ¯º€£©
œ˙ €µ•º€x£®‘™£© | 20 | 22 | 25 | °≠ |
‘¬œ˙ €∂Óy£®÷ª£© | 300 | 280 | 250 | °≠ |
£®1£©«Û≥ˆy”Îx÷ƺ‰µƒ∫Ø ˝±Ì¥Ô Ω
£®2£©∏√–¬–Õ°∞Œ¸ÀÆÕœ∞—°±√ø‘¬µƒ◊п˚»ÛŒ™w£®‘™£©£¨«Ûwπÿ”⁄xµƒ∫Ø ˝±Ì¥Ô Ω£¨≤¢÷∏≥ˆœ˙ €µ•º€Œ™∂ý…Ÿ‘™ ±¿˚»Û◊Ó¥Û£¨◊Ó¥Û¿˚»Û «∂ý…Ÿ‘™£ø
£®3£©”…”⁄∏√–¬–Õ°∞Œ¸ÀÆÕœ∞—°± –≥°–Ë«Û¡øΩœ¥Û£¨≥ߺ“”÷Ω¯––¡À∏ƒ◊∞£¨¥À ±≥¨ –¿œ∞Â∑¢œ÷Ω¯º€Ã·∏þ¡Àm‘™£¨µ±√ø‘¬œ˙ €¡ø”Îœ˙ €µ•º€»‘¬˙◊„…œ ˆ“ª¥Œ∫Ø ˝πÿœµ£¨ÀÊ◊≈œ˙¡øµƒ‘ˆ¥Û£¨◊Ó¥Û¿˚»ÛƒÐºı…Ÿ1750‘™£¨«Ûmµƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº1£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨≈◊ŒÔœþy£Ω![]() ”Îx÷·Ωª”⁄A£¨C£®A‘⁄Cµƒ◊Û≤ý£©£¨µ„B‘⁄≈◊ŒÔœþ…œ£¨∆‰∫·◊¯±ÍŒ™1£¨¡¨Ω”BC£¨BO£¨µ„FŒ™OB÷–µ„£Æ
”Îx÷·Ωª”⁄A£¨C£®A‘⁄Cµƒ◊Û≤ý£©£¨µ„B‘⁄≈◊ŒÔœþ…œ£¨∆‰∫·◊¯±ÍŒ™1£¨¡¨Ω”BC£¨BO£¨µ„FŒ™OB÷–µ„£Æ

£®1£©«Û÷±œþBCµƒ∫Ø ˝±Ì¥Ô Ω£ª
£®2£©»Ùµ„DŒ™≈◊ŒÔœþµ⁄ÀƒœÛœÞ…œµƒ“ª∏ˆ∂ص„£¨¡¨Ω”BD£¨CD£¨µ„EŒ™x÷·…œ“ª∂ص„£¨µ±°˜BCDµƒ√ʪ˝µƒ◊Ó¥Û ±£¨«Ûµ„Dµƒ◊¯±Í£¨º∞|FE©ÅDE|µƒ◊Ó¥Û÷µ£ª
£®3£©»ÁÕº2£¨»Ùµ„G”ε„Bπÿ”⁄≈◊ŒÔœþ∂‘≥∆÷·∂‘≥∆£¨÷±œþBG”Îy÷·Ωª”⁄µ„M£¨µ„N «œþ∂ŒBG…œµƒ“ª∂ص„£¨¡¨Ω”NF£¨MF£¨µ±°œNFO£Ω3°œBNF ±£¨¡¨Ω”CN£¨Ω´÷±œþBO»∆µ„O–˝◊™£¨º«–˝◊™÷–µƒ÷±œþBOŒ™B°‰O£¨÷±œþB°‰O”Î÷±œþCNΩª”⁄µ„Q£¨µ±°˜OCQŒ™µ»—¸»˝Ω«–Œ ±£¨«Ûµ„Qµƒ◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø°∞¬ø”—°±–°√˜∑÷»˝¥Œ¥”Mµÿ≥ˆ∑¢—ÿ◊≈≤ªÕ¨µƒœþ¬∑![]() œþ£¨Bœþ£¨Cœþ
œþ£¨Bœþ£¨Cœþ![]() »•Nµÿ
»•Nµÿ![]() ‘⁄√øÃıœþ¬∑…œ––Ω¯µƒ∑Ω Ω∂º∑÷Œ™¥©‘Ω¥‘¡÷°¢…ÊÀÆ––◊þ∫Õ≈ µ«’‚»˝÷÷
‘⁄√øÃıœþ¬∑…œ––Ω¯µƒ∑Ω Ω∂º∑÷Œ™¥©‘Ω¥‘¡÷°¢…ÊÀÆ––◊þ∫Õ≈ µ«’‚»˝÷÷![]() À˚…ÊÀÆ––◊þ4–° ±µƒ¬∑≥ÔÎ≈ µ«6–° ±µƒ¬∑≥Ãœýµ»
À˚…ÊÀÆ––◊þ4–° ±µƒ¬∑≥ÔÎ≈ µ«6–° ±µƒ¬∑≥Ãœýµ»![]() œþ°¢Cœþ¬∑≥Ãœýµ»£¨∂º±»Aœþ¬∑≥Ã∂ý
œþ°¢Cœþ¬∑≥Ãœýµ»£¨∂º±»Aœþ¬∑≥Ã∂ý![]() £¨Aœþ◊Ð ±º‰µ»”⁄Cœþ◊Ð ±º‰µƒ
£¨Aœþ◊Ð ±º‰µ»”⁄Cœþ◊Ð ±º‰µƒ![]() £¨À˚”√¡À3–° ±¥©‘Ω¥‘¡÷°¢2–° ±…ÊÀÆ––◊þ∫Õ2–° ±≈ µ«◊þÕÍAœþ£¨‘⁄Bœþ÷–¥©‘Ω¥‘¡÷°¢…ÊÀÆ––◊þ∫Õ≈ µ«À˘”√ ±º‰∑÷±±»Aœþ…œ…˝¡À
£¨À˚”√¡À3–° ±¥©‘Ω¥‘¡÷°¢2–° ±…ÊÀÆ––◊þ∫Õ2–° ±≈ µ«◊þÕÍAœþ£¨‘⁄Bœþ÷–¥©‘Ω¥‘¡÷°¢…ÊÀÆ––◊þ∫Õ≈ µ«À˘”√ ±º‰∑÷±±»Aœþ…œ…˝¡À![]() £¨
£¨![]() £¨
£¨![]() £¨»ÙÀ˚”√¡Àx–° ±¥©‘Ω¥‘¡÷°¢y–° ±…ÊÀÆ––◊þ∫Õz–° ±≈ µ«◊þÕÍCœþ£¨«“x£¨y£¨z∂ºŒ™’˝’˚ ˝£¨‘Ú
£¨»ÙÀ˚”√¡Àx–° ±¥©‘Ω¥‘¡÷°¢y–° ±…ÊÀÆ––◊þ∫Õz–° ±≈ µ«◊þÕÍCœþ£¨«“x£¨y£¨z∂ºŒ™’˝’˚ ˝£¨‘Ú![]() ______£Æ
______£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
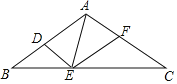
°æƒø°ø»ÁÕº£¨°˜ABC÷–£¨AB=AC=15£¨°œBAC=120°„£¨–°√˜“™Ω´∏√»˝Ω«–Œ∑÷∏Ó≥…¡Ω∏ˆ÷±Ω«»˝Ω«–Œ∫Õ¡Ω∏ˆµ»—¸»˝Ω«–Œ£¨À˚œÎ≥ˆ¡À»Áœ¬∑Ω∞∏£∫‘⁄AB…œ»°µ„D£¨π˝µ„Dª≠DE°ŒACΩªBC”⁄µ„E£¨¡¨Ω·AE£¨‘⁄AC…œ»°∫œ µƒµ„F£¨¡¨Ω·EFø…µ√µΩ4∏ˆ∑˚∫œÃıº˛µƒ»˝Ω«–Œ£¨‘Ú¬˙◊„Ãıº˛µƒAF≥§ «______£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com