
【题目】如图,△ABC中,AB=AC=15,∠BAC=120°,小明要将该三角形分割成两个直角三角形和两个等腰三角形,他想出了如下方案:在AB上取点D,过点D画DE∥AC交BC于点E,连结AE,在AC上取合适的点F,连结EF可得到4个符合条件的三角形,则满足条件的AF长是______.
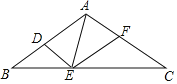
【答案】7.5
【解析】
根据已知条件可判定△BDE和△EFC始终为等腰三角形,并可求得∠AFE=∠ADE=30°,若△AEF和△ADE为等腰三角形,则必为等边三角形.将求AF的长度转化为求AE的长度.然后通过解Rt△AEC即可.也可以用直角三角形斜边上的中线等于斜边的一半求解.
解:如图
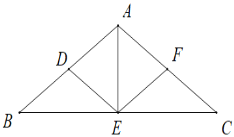
∵AB=AC
∴∠B=∠C
∵∠BAC=120°,∠BAC+∠B+∠C=180°
∴∠B=∠C=30°
∵DE∥∥AC,EF∥AB
∴∠DEB=∠C=30°,∠FEC=∠B=30°
∴∠B=∠DEB,∠C=∠FEC
∴△DBE,△FEC是等腰三角形
∵AB∥EF
∴∠EFA+∠BAC=180
∴∠EFA=60°
∵△AEF是等腰三角形
∴△AEF是等边三角形
∴AF=AE,∠AEF=∠EFA=60°
∴∠AEC=∠AEF+∠FEC=90°
在Rt△AEC中,AC=15,∠C=30°,∠AEC=90°
![]()
∴AF=7.5
故答案为7.5


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】2018年平昌冬奥会在2月9日到25日在韩国平昌郡举行。为了调查中学生对冬奥会比赛项目的了解程度,某中学在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解 B、比较了解 C、基本了解 D、不了解。根据调查统计结果,绘制了如图所示的不完整的三种统计图表。
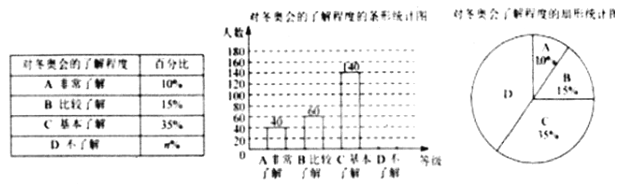
(1)本次调查的样本容量是 ,n= ;
(2)请补全条形统计图;
(3)学校准备开展冬奥会的知识竞赛,该校共有4000名学生,请你估计这所学校本次竞赛“非常了解”和“比较了解”的学生总数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA,PB是⊙O的两条切线,切点分别为A,B,OP交AB于点C,OP=13,sin∠APC=![]() .
.
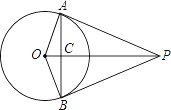
(1)求⊙O的半径;
(2)求弦AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
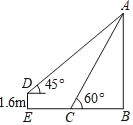
【题目】小明想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好在C处且与地面成60°角,小明拿起绳子末端,后退至E处,拉直绳子,此时绳子末端D距离地面1.6m且绳子与水平方向成45°角.
(1)填空:AD_____AC(填“>”,“<”,“=”).
(2)求旗杆AB的高度.
(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,结果精确到0.1m).
≈1.73,结果精确到0.1m).
查看答案和解析>>
科目:初中数学 来源: 题型:
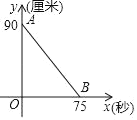
【题目】某工地需要利用炸药实施爆破,操作人员点燃导火线后,要在炸药爆炸前跑到300米以外的安全区域,炸药导火线的长度y(厘米)与燃烧的时间x(秒)之间的函数关系如图所示.
(1)请写出点B的实际意义,
(2)求y与x之间的函数关系式,并写出自变量的取值范围.
(3)问操作人员跑步的速度必须超过多少,才能保证安全.
查看答案和解析>>
科目:初中数学 来源: 题型:
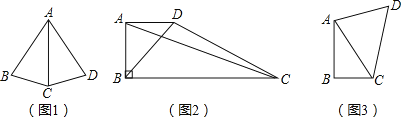
【题目】定义:如果一个四边形存在一条对角线,使得这条对角线是四边形某两边的比例中项,则称这个四边形为“闪亮四边形”,这条对角线称为“亮线”.如图1,四边形ABCD中,AB=AC=AD,满足AC2=ABAD,四边形ABCD是闪亮四边形,AC是亮线.
(1)以下说法正确的是______(填写序号)
①正方形不可能是闪亮四边形;
②矩形中存在闪亮四边形;
③若一个菱形是闪亮四边形,则必有一个内角是60°.
(2)如图2,四边形ABCD中,AD∥BC,∠ABC=90°,AD=9,AB=12,CD=20,判断哪一条线段是四边形ABCD的亮线?请你作出判断并说明理由.
(3)如图3,AC是闪亮四边形ABCD的唯一亮线,∠ABC=90°,∠D=60°,AB=4,BC=2,请直接写出线段AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
观察与思考:阅读下列材料,并解决后面的问题.在锐角![]() 中,
中,![]() 、
、![]() 、
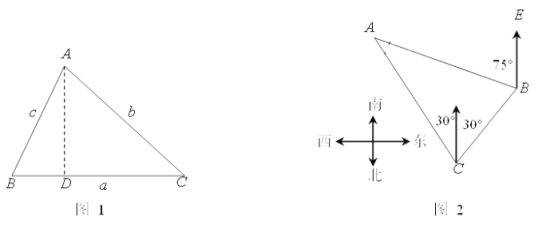
、![]() 的对边分别是a、b、c,过A作
的对边分别是a、b、c,过A作![]() 于D(如图),则
于D(如图),则![]() ,
,![]() ,即
,即![]() ,
,![]() ,于是
,于是![]() ,即
,即![]() .同理有:
.同理有:![]() ,
,![]() ,所以
,所以![]() .
.
即:在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.根据上述材料,完成下列各题.
(1)如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
(2)如图,一货轮在C处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以60海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西75°的方向上(如图),求此时货轮距灯塔A的距离AB.
(3)在(2)的条件下,试求75°的正弦值.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
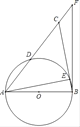
【题目】如图,在等腰△ABC中,AB=BC,以AB为直径的半圆分别交AC、BC于点D、E两点,BF与⊙O相切于点B,交AC的延长线于点F.
(1)求证:D是AC的中点;
(2)若AB=12,sin∠CAE=![]() ,求CF的值.
,求CF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
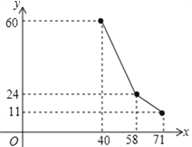
【题目】国家为支持大学生创业,提供小额无息贷款,学生王芳享受政策无息贷款36000元用来代理品牌服装的销售.已知该品牌服装进价每件40元,日销售y(件)与销售价x(元/件)之间的关系如图所示(实线),每天付员工的工资每人每天82元,每天应支付其它费用106元.
(1)求日销售y(件)与销售价x (元/件)之间的函数关系式;
(2)若暂不考虑还贷,当某天的销售价为48元/件时,收支恰好平衡(收入=支出),求该店员工人数;
(3)若该店只有2名员工,则该店至少需要多少天才能还清贷款,此时,每件服装的价格应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com