
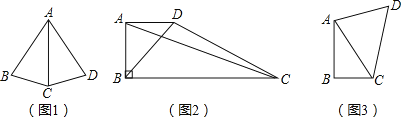
����Ŀ�����壺���һ���ı��δ���һ���Խ��ߣ�ʹ�������Խ������ı���ij���ߵı�������������ı���Ϊ�������ı������������Խ��߳�Ϊ������������ͼ1���ı���ABCD�У�AB=AC=AD������AC2=ABAD���ı���ABCD�������ı��Σ�AC�����ߣ�
��1������˵����ȷ����______����д��ţ�
�������β������������ı��Σ�
�ھ����д��������ı��Σ�
����һ�������������ı��Σ������һ���ڽ���60����
��2����ͼ2���ı���ABCD�У�AD��BC����ABC=90����AD=9��AB=12��CD=20���ж���һ���߶����ı���ABCD�����ߣ����������жϲ�˵�����ɣ�
��3����ͼ3��AC�������ı���ABCD��Ψһ���ߣ���ABC=90������D=60����AB=4��BC=2����ֱ��д���߶�AD�ij���
���𰸡�(1)�١��ۣ�(2)![]() Ϊ�ı���
Ϊ�ı���![]() �����ߣ�(3)
�����ߣ�(3)![]() .
.
��������
��1�����������ı��εĶ���һһ�жϼ��ɣ�
��2����ͼ2�У���DH��BC��H�����BD��AC�����жϣ�
��3����취֤����ADC�ǵȱ������μ��ɽ�����⣮
�⣺(1) ���������εı߳�Ϊa����Խ��߳�Ϊ![]() a��
a��
![]() ��
��
�������β������������ı��Σ��ʢ���ȷ
����ͼ���У��ı���ABCD�Ǿ��Σ�AE��AC��E������������������ı��Σ�
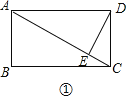
��AC2=ADCD��
![]() ��
��
��DE=AC��
��AC��AD��DE����Ȼ��DE=ACì�ܣ����費������
����β������������ı��Σ��ʢڴ���
����ͼ���У��ı���ABCD�����Σ�
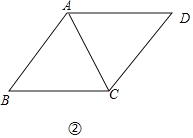
���ı���ABC���������ı��Σ�
������AC2=ADCD��
���ı���ABCD�����Σ�
��AD=CD��
��AC=AD=CD��
���ADC�ǵȱ������Σ�
���D=60����
����һ�������������ı��Σ������һ���ڽ���60�����ʢ���ȷ��
�ʴ�Ϊ�٢�
(2)����![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
��![]() ��
��![]() ����
����![]()
��![]() �����ı���
�����ı���![]() Ϊ����
����
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
�֡�![]() ��
��![]()
��![]() ��
��![]()
��ʱ![]() ��
��![]()
��![]() ����
����![]() Ϊ�ı���
Ϊ�ı���![]() �����ߣ�
�����ߣ�
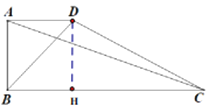
(3) ��ͼ3�У���CH��AD��H��
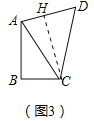
��DH=CDcos��D��CH=CDsin��D��AH=AD-CDcos��D��
��AC2=AH2+CH2=��AD-CDcos��D��2+��CDsin��D��2
=AD2+CD2-2ADCDcos��D
=AD2+CD2-ADCD��
��AC2=ADCD��
��AD2-2ADCD+CD2=0��
�ࣨAD-CD��2=0��
��AD=CD���ߡ�D=60����
���ACD�ǵȱ������Σ�
![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y��![]() ��x�ύ��A��C��A��C����ࣩ����B���������ϣ��������Ϊ1������BC��BO����FΪOB�е㣮
��x�ύ��A��C��A��C����ࣩ����B���������ϣ��������Ϊ1������BC��BO����FΪOB�е㣮

��1����ֱ��BC�ĺ�������ʽ��
��2������DΪ�����ߵ��������ϵ�һ�����㣬����BD��CD����EΪx����һ���㣬����BCD����������ʱ�����D�����꣬��|FE��DE|�����ֵ��
��3����ͼ2������G���B���������߶Գ���Գƣ�ֱ��BG��y�ύ�ڵ�M����N���߶�BG�ϵ�һ���㣬����NF��MF������NFO��3��BNFʱ������CN����ֱ��BO�Ƶ�O��ת������ת�е�ֱ��BOΪB��O��ֱ��B��O��ֱ��CN���ڵ�Q������OCQΪ����������ʱ�����Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ��ֱ��������ֽƬOAB��������AOB=90�㣬OA=2��OB=4����ͼ������ֽƬ������ƽ��ֱ������ϵ�У��۵���ֽƬ���ۺ����OB���ڵ�C�����AB���ڵ�D��
��1�����۵���ʹ��B���A�غϣ����C�����ꣻ
��2�����۵����B���ڱ�OA�ϵĵ�ΪB������OB��=x��OC=y����д��y����x�ĺ�������ʽ����ȷ��y��ȡֵ��Χ��
��3�����۵����B���ڱ�OA�ϵĵ�ΪB������ʹB��D//OB�����ʱ��C�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
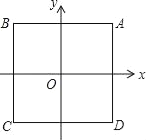
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���O�DZ߳�Ϊ2��������ABCD�����ģ�����y����x��h��2��ͼ����������ABCD�й����㣬��h��ȡֵ��Χ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
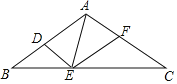
����Ŀ����ͼ����ABC�У�AB=AC=15����BAC=120����С��Ҫ���������ηָ������ֱ�������κ��������������Σ�����������·�������AB��ȡ��D������D��DE��AC��BC�ڵ�E������AE����AC��ȡ���ʵĵ�F������EF�ɵõ�4�����������������Σ�������������AF����______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0����ͼ����x�����������A��B�ĺ�����ֱ�Ϊ��3��1����y�ύ�ڵ�C�������ĸ����ۣ���16a+4b+c��0������P����5��y1����Q��![]() ��y2���Ǻ���ͼ���ϵ����㣬��y1��y2����c=��3a��������ABC�ǵ��������Σ���b=��
��y2���Ǻ���ͼ���ϵ����㣬��y1��y2����c=��3a��������ABC�ǵ��������Σ���b=��![]() ��
��![]() ��������ȷ����_____�����뽫��ȷ���۵����ȫ�����ں����ϣ�
��������ȷ����_____�����뽫��ȷ���۵����ȫ�����ں����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���֪����������y��![]() x��ͼ���뷴��������y��
x��ͼ���뷴��������y��![]() ��ͼ����A��a����2����B���㣮
��ͼ����A��a����2����B���㣮
��1�����������ı���ʽ�͵�B�����ꣻ
��2��P�ǵ�һ�����ڷ���������ͼ����һ�㣬����P��y���ƽ���ߣ���ֱ��AB�ڵ�C������PO������POC�����Ϊ3�����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
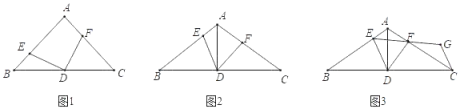
����Ŀ������ABC�У�AB��AC����D��BC�е㣬��EDF���߷ֱ��߶�AB�ڵ�E�����߶�AC�ڵ�F���ҡ�EDF+��BAC��180��
��1����ͼ1������EDF��90��ʱ����֤��BE��AF��
��2����ͼ2������EDF��60��ʱ����֤��AE+AF��AD��
��3����ͼ3���ڣ�2���������£�����EF���ӳ�EF����G��ʹFG��EF������CG����BE��5��CF��4����CG�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���װ��Ϊ�˵���ӪҵԱ�Ļ����ԣ�����ʵ��Ŀ�����������Ŀ����ɵ������ӪҵԱ�����ʵ��Ľ�����Ϊ��ȷ��һ���ʵ���������Ŀ�꣬�̳���װ��ͳ����ÿλӪҵԱ��ij�µ����۶��λ����Ԫ�����������£�
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
����30�����ݰ����3���з��飬�������������ͷ������£�
Ƶ���ֲ���
��� | һ | �� | �� | �� | �� | �� | �� |
���۶� |
|
|
|
|
|
|
|
Ƶ�� | 7 | 9 | 3 |
| 2 |
| 2 |
���ݷ�����
ƽ���� | ���� | ��λ�� |
20.3 |
| 18 |
�����������Ϣ����������⣺
��1����գ�a=������b=������c=������
��2�����������۶����25��Ԫȷ��Ϊ����Ŀ�꣬��������λӪҵԱ��ý�����
��3��������һ�����ҵ�ӪҵԱ���ܴﵽ����Ŀ�꣬����Ϊ�����۶Ϊ���ٺ��ʣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com