
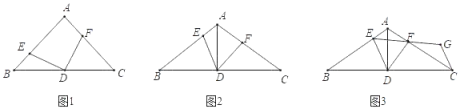
【题目】在△ABC中,AB=AC,点D是BC中点,∠EDF两边分别交线段AB于点E,交线段AC于点F,且∠EDF+∠BAC=180°
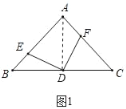
(1)如图1,当∠EDF=90°时,求证:BE=AF;
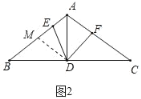
(2)如图2,当∠EDF=60°时,求证:AE+AF=AD;
(3)如图3,在(2)的条件下,连接EF并延长EF至点G,使FG=EF,连接CG,若BE=5,CF=4,求CG的长度.
【答案】(1)证明见解析;(2)证明见解析;(3)CG=![]() .
.
【解析】
1)由等腰三角形的性质得出AD⊥BC,AD=![]() BC=BD=CD,∠B=∠C=45°,∠DAF=
BC=BD=CD,∠B=∠C=45°,∠DAF=![]() ∠BAC=45°,求出∠B=∠DAF,∠BDE=∠ADF,由ASA证明△BDE≌△ADF,即可得出结论;
∠BAC=45°,求出∠B=∠DAF,∠BDE=∠ADF,由ASA证明△BDE≌△ADF,即可得出结论;
(2)取AB的中点M,连接DM,由直角三角形的性质得出DM=![]() AB=BM=AM,证出△ADM是等边三角形,得出AM=DM=AD,∠AMD=∠ADM=60°,证明△DEM≌△DFA,得出MD=AF,即可得出结论;
AB=BM=AM,证出△ADM是等边三角形,得出AM=DM=AD,∠AMD=∠ADM=60°,证明△DEM≌△DFA,得出MD=AF,即可得出结论;
(3)作EH⊥BC于H,FM⊥BC于M,GN⊥BC于N,则EH∥FM∥GN,由(2)得:AE+AF=AD,由等腰三角形的性质得出∠B=∠ACB=30°,AD⊥BC,∠ADB=∠ADC=90°,由直角三角形的性质得出AD=![]() AB,BD=CD=
AB,BD=CD=![]() AD,EH=
AD,EH=![]() BE=
BE=![]() ,FM=
,FM=![]() CF=2,BH=
CF=2,BH=![]() EH=
EH=![]() ,CM=
,CM=![]() FM=2
FM=2![]() ,求出AB=6,得出AD=3,BD=CD=3
,求出AB=6,得出AD=3,BD=CD=3![]() ,∴DH=BDBH=
,∴DH=BDBH=![]() ,DM=CDCM=
,DM=CDCM=![]() ,求出HM=DH+DM=
,求出HM=DH+DM=![]() ,证出FM是梯形EHNG的中位线,HM=MN,得出2FM=EH+GN,MN=
,证出FM是梯形EHNG的中位线,HM=MN,得出2FM=EH+GN,MN=![]() ,CN=CDDMMN=
,CN=CDDMMN=![]() ,求出GN=
,求出GN=![]() ,在Rt△CGN中,由勾股定理即可求出CG的长.
,在Rt△CGN中,由勾股定理即可求出CG的长.
(1)证明:连接AD,如图1所示:
∵∠EDF+∠BAC=180°,∠EDF=90°,
∴∠BAC=90°,
∵AB=AC,点D是BC中点,
∴AD⊥BC,AD=![]() BC=BD=CD,∠B=∠C=45°,∠DAF=
BC=BD=CD,∠B=∠C=45°,∠DAF=![]() ∠BAC=45°,
∠BAC=45°,
∴∠B=∠DAF,
∵∠EDF=90°,
∴∠BDE=∠ADF,
在△BDE和△ADF中,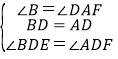 ,
,
∴△BDE≌△ADF(ASA),
∴BE=AF;
(2)证明:取AB的中点M,连接DM,如图2所示:
∵AD⊥BC,M是AB的中点,
∴DM=![]() AB=BM=AM,
AB=BM=AM,
∵∠EDF+∠BAC=180°,∠EDF=60°,
∴∠BAC=120°,
∵AB=AC,点D是BC中点,
∴∠BAD=∠CAD=![]() ∠BAC=60°,
∠BAC=60°,
∴△ADM是等边三角形,
∴AM=DM=AD,∠AMD=∠ADM=60°,
∴∠MDE=∠ADF,
在△DEM和△DFA中,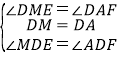 ,
,
∴△DEM≌△DFA(ASA),
∴MD=AF,
∵AE+ME=AM=AD,
∴AE+AF=AD;
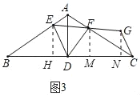
(3)解:作EH⊥BC于H,FM⊥BC于M,GN⊥BC于N,如图3所示:
则EH∥FM∥GN,
由(2)得:AE+AF=AD,
∵BE=5,CF=4,AB+AC=BE+AE+AF+CF=BE+AD+CF=5+AD+4=9+AD,
∵∠BAC=120°,AB=AC,点D是BC中点,
∴∠B=∠ACB=30°,AD⊥BC,∠ADB=∠ADC=90°,
∴AD=![]() AB
AB![]() AD,EH=
AD,EH=![]() BE=
BE=![]() ,FM=
,FM=![]() CF=2,BH=
CF=2,BH=![]() EH=
EH=![]() ,CM=
,CM=![]() FM=2
FM=2![]() ,
,
∴2AB=9+![]() AB,
AB,
解得:AB=6,
∴AD=3,BD=CD=3![]() ,
,
∴DH=BD﹣BH=![]() ,DM=CD﹣CM=
,DM=CD﹣CM=![]() ,
,
∴HM=DH+DM=![]() ,
,
∵EH∥FM∥GN,EF=FG,
∴FM是梯形EHNG的中位线,HM=MN,
∴2FM=EH+GN,MN=![]() ,CN=CD﹣DM﹣MN=3
,CN=CD﹣DM﹣MN=3![]() ﹣
﹣![]() ﹣
﹣![]() =
=![]() ,2×2=
,2×2=![]() +GN,
+GN,
∴GN=![]() ,
,
在Rt△CGN中,由勾股定理得:CG=![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料
计算:(1﹣![]() ﹣
﹣![]() )×(
)×(![]() +
+![]() )﹣(1﹣
)﹣(1﹣![]() ﹣
﹣![]() )(
)(![]() +
+![]() ),令
),令![]() +
+![]() =t,则:
=t,则:
原式=(1﹣t)(t+![]() )﹣(1﹣t﹣
)﹣(1﹣t﹣![]() )t=t+
)t=t+![]() ﹣t2﹣
﹣t2﹣![]() +t2=
+t2=![]()
在上面的问题中,用一个字母代表式子中的某一部分,能达到简化计算的目的,这种思想方法叫做“换元法”,请用“换元法”解决下列问题:
(1)计算:(1﹣![]() ﹣
﹣![]() )×(
)×(![]() +
+![]() )﹣(1﹣
)﹣(1﹣![]() ﹣
﹣![]() )×(
)×(![]() +
+![]() )
)
(2)因式分解:(a2﹣5a+3)(a2﹣5a+7)+4
(3)解方程:(x2+4x+1)(x2+4x+3)=3
查看答案和解析>>
科目:初中数学 来源: 题型:
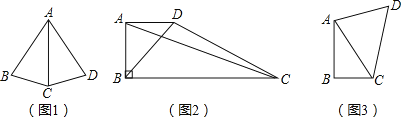
【题目】定义:如果一个四边形存在一条对角线,使得这条对角线是四边形某两边的比例中项,则称这个四边形为“闪亮四边形”,这条对角线称为“亮线”.如图1,四边形ABCD中,AB=AC=AD,满足AC2=ABAD,四边形ABCD是闪亮四边形,AC是亮线.
(1)以下说法正确的是______(填写序号)
①正方形不可能是闪亮四边形;
②矩形中存在闪亮四边形;
③若一个菱形是闪亮四边形,则必有一个内角是60°.
(2)如图2,四边形ABCD中,AD∥BC,∠ABC=90°,AD=9,AB=12,CD=20,判断哪一条线段是四边形ABCD的亮线?请你作出判断并说明理由.
(3)如图3,AC是闪亮四边形ABCD的唯一亮线,∠ABC=90°,∠D=60°,AB=4,BC=2,请直接写出线段AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
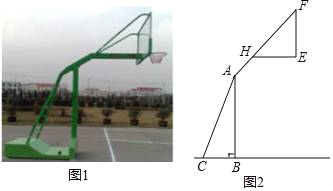
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知AB⊥BC于点B,底座BC的长为1米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC,EF⊥EH于点E,已知AH长![]() 米,HF长
米,HF长![]() 米,HE长1米.
米,HE长1米.
(1)求篮板底部支架HE与支架AF所成的角∠FHE的度数.
(2)求篮板底部点E到地面的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
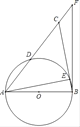
【题目】如图,在等腰△ABC中,AB=BC,以AB为直径的半圆分别交AC、BC于点D、E两点,BF与⊙O相切于点B,交AC的延长线于点F.
(1)求证:D是AC的中点;
(2)若AB=12,sin∠CAE=![]() ,求CF的值.
,求CF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】共享单车为人们的生活带来了极大的便利.如图,一辆单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A,B之间的距离为49cm,现测得AC,BC与AB的夹角分别为45°,68°.若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为5cm,求点E到地面的距离.(结果保留一位小数,参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.50.)

查看答案和解析>>
科目:初中数学 来源: 题型:
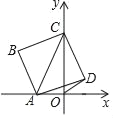
【题目】如图,点A是x轴负半轴上的一个动点,点C在y轴上,以AC为对角线画正方形ABCD,已知点C的坐标是C(0,4),设点A的坐标为A(n,0),连接OD,当OD=![]() 时,n=_____.
时,n=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:(1)如图①,在Rt△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC,则线段BC,DC,EC之间满足的等量关系式为 ;
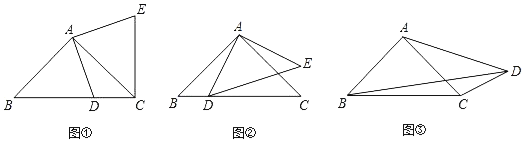
探索:(2)如图②,在Rt△ABC与Rt△ADE中,AB=AC,AD=AE,将△ADE绕点A旋转,使点D落在BC边上,试探索线段AD,BD,CD之间满足的等量关系,并证明你的结论;
应用:(3)如图③,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°.若BD=9,CD=3,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
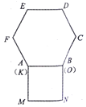
【题目】已知正方形![]() 和正六边形
和正六边形 ![]() 边长均为1,如图所示,把正方形放置在正六边形外,使
边长均为1,如图所示,把正方形放置在正六边形外,使![]() 边与
边与![]() 边重合,按下列步骤操作:将正方形在正六边形外绕点
边重合,按下列步骤操作:将正方形在正六边形外绕点![]() 逆时针旋转,使
逆时针旋转,使![]() 边与
边与![]() 边重合,完成第一次旋转再绕点
边重合,完成第一次旋转再绕点![]() 逆时针旋转,使
逆时针旋转,使![]() 边与
边与![]() 边重合,完成第二次旋转;此时点
边重合,完成第二次旋转;此时点![]() 经过路径的长为_________:若按此方式旋转,共完成六次,在这个过程中,点
经过路径的长为_________:若按此方式旋转,共完成六次,在这个过程中,点![]() 之间距离的最大值是____.
之间距离的最大值是____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com