
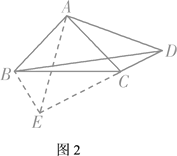
����Ŀ�����⣺��1����ͼ�٣���Rt��ABC�У�AB��AC��DΪBC����һ�㣨�����B��C�غϣ������߶�AD�Ƶ�A��ʱ����ת90��õ�AE������EC�����߶�BC��DC��EC֮������ĵ�����ϵʽΪ�� ����
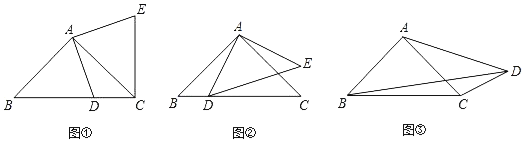
̽������2����ͼ�ڣ���Rt��ABC��Rt��ADE�У�AB��AC��AD��AE������ADE�Ƶ�A��ת��ʹ��D����BC���ϣ���̽���߶�AD��BD��CD֮������ĵ�����ϵ����֤����Ľ��ۣ�
Ӧ�ã���3����ͼ�ۣ����ı���ABCD�У���ABC����ACB����ADC��45�㣮��BD��9��CD��3����AD�ij���
���𰸡���1��BC��DC��EC����2��BD2��CD2��2AD2����3��AD��6.
��������
��1����֤��BAD�ա�CAE�����ɵõ�BC��DC��EC
��2������CE����֤��BAD�ա�CAE���ٵõ�ED��![]() AD��Ȼ����Rt��ECD�����ù��ɶ�������������ϵ��
AD��Ȼ����Rt��ECD�����ù��ɶ�������������ϵ��
��3�����߶�AD�Ƶ�A˳ʱ����ת90���õ�AE������CE��BE����֤��ABE�ա�ACD����������Rt��BED�У��ɹ��ɶ�������DE2��BD2��BE2����2AD2��BD2��CD2���ٽ��AD�ij�����.
�⣺(1)BC��DC��EC��
�ߡ�BAC����DAE��90����
���BAC����DAC����DAE����DAC������BAD����CAE.
�ڡ�BAD�͡�CAE�У�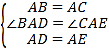
���BAD�ա�CAE(SAS)��
��BD��CE��
��BC��BD��CD��EC��CD��
(2)BD2��CD2��2AD2.
֤�����£�
����CE�����ͼ1��ʾ��
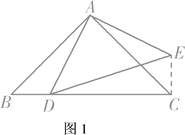
�ߡ�BAC����BAD����DAC��90����AB��AC��
���ABC����ACB��45��.
�ߡ�DAE����CAE����DAC��90����
���BAD����CAE.
�ڡ�BAD�͡�CAE�У�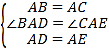
���BAD�ա�CAE(SAS)��
��BD��CE����ACE����ABC��45����
���BCE����ACB����ACE��90��.
�ߡ�EAD��90����AE��AD��
��ED��![]() AD��
AD��
��Rt��ECD�У��ɹ��ɶ�����
��ED2��CE2��CD2��
��BD2��CD2��2AD2.
(3)���߶�AD�Ƶ�A˳ʱ����ת90���õ�AE������CE��BE��
���ͼ2��ʾ����AE��AD����EAD��90����
���EAD�ǵ���ֱ�������Σ�
��DE��![]() AD����AED��45��.
AD����AED��45��.
�ߡ�ABC����ACB��ADC��45����
���BAC��90����AB��AC��
ͬ(2)�ķ�������֤�á�ABE�ա�ACD��
��BE��CD����AEB����ADC��45����
���BEC����AEB����AED��90��.
��Rt��BED�У��ɹ��ɶ�������DE2��BD2��BE2��
��2AD2��BD2��CD2.
��BD��9��CD��3��
��2AD2��92��32��72��
��AD��6(��ֵ����ȥ)��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
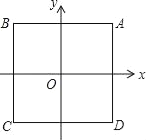
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���O�DZ߳�Ϊ2��������ABCD�����ģ�����y����x��h��2��ͼ����������ABCD�й����㣬��h��ȡֵ��Χ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
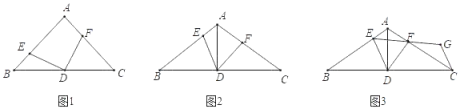
����Ŀ������ABC�У�AB��AC����D��BC�е㣬��EDF���߷ֱ��߶�AB�ڵ�E�����߶�AC�ڵ�F���ҡ�EDF+��BAC��180��
��1����ͼ1������EDF��90��ʱ����֤��BE��AF��
��2����ͼ2������EDF��60��ʱ����֤��AE+AF��AD��
��3����ͼ3���ڣ�2���������£�����EF���ӳ�EF����G��ʹFG��EF������CG����BE��5��CF��4����CG�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������ABCֽƬ����λ��EH�۵���ʹ��A�ԳƵ�D����BC���ϣ��ٽ�ֽƬ�ֱ��ص�����BED�͵�����DHC�ĵױ��ϵĸ���EF��HG�۵����۵��������������ƴ���γ�һ�����Σ����Ƶأ��Զ���ν����۵��������ۺ��ͼ��ǡ��ƴ�ϳ�һ����϶�����ص��ľ��Σ������ľ��γ�Ϊ���Ͼ��Σ�




��1������ABCDֽƬ��ͼ2�ķ�ʽ�۵���һ�����Ͼ���AEFG��������γɵ��ۺ۷ֱ����߶�_______��_________��S����AEFG��S��ABCD=__________��
��2����ABCDֽƬ������ͼ3�ķ�ʽ�۵���һ�����Ͼ���EFGH����EF=5��EH=12����AD�ij���
��3����ͼ4���ı���ABCDֽƬ����AD��BC��AD��BC��AB��BC��AB=8��CD=10��С���Ѹ�ֽƬ�۵����õ����������Σ������������һ�ֵ��������ε�ʾ��ͼ�������AD��BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
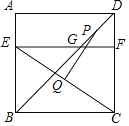
����Ŀ����ͼ��������ABCD�ı߳�Ϊ12����E�ڱ�AB�ϣ�BE=8������E��EF��BC���ֱ�BD��CD��G��F���㣮����P��Q�ֱ�ΪDG��CE���е㣬��PQ�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ѧ��ѧ¥������һ��Сɽ��ȥ�ꡰ��ͨ����˾��ɽ���Ͻ�����ͨѶ�������ס�����λͬѧ���������ĸ߶ȣ������ò�����������²��������ڽ�ѧ¥��A���������M������Ϊ��������N������Ϊ��������һ¥B��ֻ����������M���������Ϊ����������������������֪��¥��AB��20m��ͨ������ã�tan����0.5723��tan����0.2191��tan����0.7489����������⼸�����ݣ����ͼ������������߶�MN��ֵ��
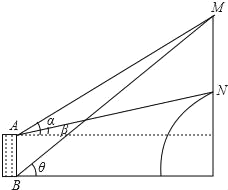
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���װ��Ϊ�˵���ӪҵԱ�Ļ����ԣ�����ʵ��Ŀ�����������Ŀ����ɵ������ӪҵԱ�����ʵ��Ľ�����Ϊ��ȷ��һ���ʵ���������Ŀ�꣬�̳���װ��ͳ����ÿλӪҵԱ��ij�µ����۶��λ����Ԫ�����������£�
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
����30�����ݰ����3���з��飬�������������ͷ������£�
Ƶ���ֲ���
��� | һ | �� | �� | �� | �� | �� | �� |
���۶� |
|
|
|
|
|
|
|
Ƶ�� | 7 | 9 | 3 |
| 2 |
| 2 |
���ݷ�����
ƽ���� | ���� | ��λ�� |
20.3 |
| 18 |
�����������Ϣ����������⣺
��1����գ�a=������b=������c=������
��2�����������۶����25��Ԫȷ��Ϊ����Ŀ�꣬��������λӪҵԱ��ý�����
��3��������һ�����ҵ�ӪҵԱ���ܴﵽ����Ŀ�꣬����Ϊ�����۶Ϊ���ٺ��ʣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У����ڵ�
�У����ڵ�![]() ��
��![]() ���������¶��壺��
���������¶��壺��![]() �ϴ���һ��
�ϴ���һ��![]() ����
����![]() �غϣ�ʹ��
�غϣ�ʹ��![]() ����ֱ��
����ֱ��![]() �ĶԳƵ�
�ĶԳƵ�![]() ��
��![]() �ϣ����
�ϣ����![]() Ϊ
Ϊ![]() �ķ���㣮��ͼΪ
�ķ���㣮��ͼΪ![]() �ķ����
�ķ����![]() ��ʾ��ͼ��
��ʾ��ͼ��
��1����֪��![]() ������Ϊ
������Ϊ![]() ��
��![]() �İ뾶Ϊ
�İ뾶Ϊ![]() ��
��
���ڵ�![]() ��
��![]() ��
��![]() ��
�У�![]() �ķ������____________��
�ķ������____________��
�ڵ�![]() ��ֱ��
��ֱ��![]() �ϣ���
�ϣ���![]() Ϊ
Ϊ![]() �ķ���㣬���
�ķ���㣬���![]() �ĺ������ȡֵ��Χ��
�ĺ������ȡֵ��Χ��
��2��![]() ��Բ����
��Բ����![]() ���ϣ��뾶Ϊ
���ϣ��뾶Ϊ![]() ��
��![]() ���ϴ��ڵ�
���ϴ��ڵ�![]() ��
��![]() �ķ���㣬ֱ��д��Բ��
�ķ���㣬ֱ��д��Բ��![]() �ĺ�����
�ĺ�����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
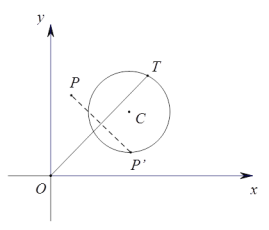
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����л���ͳ�Ļ���ijУ��֯���꼶1000��ѧ���μӺ�����д������Ϊ�˽�ѧ��������д�����������������˲���ѧ���ijɼ����÷�ȡ������������Ϊ100�֣�����ͳ�Ʒ�������������ͼ����
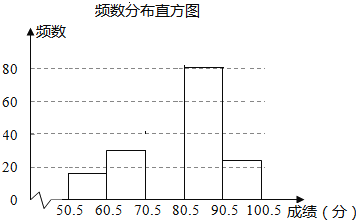
��� | ������ | Ƶ�� | Ƶ�� |
һ | 50.5��60.5 | 16 | 0.08 |
�� | 60.5��70.5 | 30 | 0.15 |
�� | 70.5��80.5 | m | 0.25 |
�� | 80.5��90.5 | 80 | n |
�� | 90.5��100.5 | 24 | 0.12 |
���������ͼ���ṩ����Ϣ��������п��⣺
��1�������������______��ѧ�������е���m=______��n=______���������гɼ�����λ�����ڵ�______���ڣ�����������ͳ��ͼ���������С������顱����Ӧ���ε�Բ�ĽǵĶ�����______
��2����ȫƵ��ֱ��ͼ��
��3�����ɼ�����80��Ϊ���㣬������Ƹ�У���꼶ѧ���к�����д���������������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com