
【题目】如图,点A是x轴负半轴上的一个动点,点C在y轴上,以AC为对角线画正方形ABCD,已知点C的坐标是C(0,4),设点A的坐标为A(n,0),连接OD,当OD=![]() 时,n=_____.
时,n=_____.
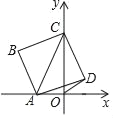
【答案】-2
【解析】
先求得OD与y轴的夹角为45°,然后依据OD的长,可求得OF和DF的长,作辅助线,构建全等三角形,再证明△AFD≌△DEC,从而可得到AF=DE=3,从而可得到点A的坐标.
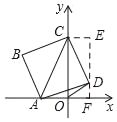
解:如图所示:过点D作EF⊥x轴于F,过C作CE⊥EF于E,
∵四边形ABCD为正方形,
∴A、B、C、D四点共圆,∠DAC=45°.
又∵∠COA=90°,
∴点O也在这个圆上,
∴∠COD=∠CAD=45°.
又∵OD=![]() ,
,
∴OF=DF=1.
∵C(0,4),
∴OC=EF=4,
∴DE=4﹣1=3,
∵四边形ABCD为正方形,
∴AD=CD,
∵∠ADC=90°,
∴∠ADF+∠CDE=∠CDE+∠DCE=90°,
∴∠ADF=∠DCE,
∵∠AFD=∠DEC=90°,
∴△AFD≌△DEC(SAS),
∴AF=DE=3,
∴AO=2,
∴A(﹣2,0),即n=﹣2;
故答案为:﹣2.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】已知一个直角三角形纸片OAB,其中∠AOB=90°,OA=2,OB=4.如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边OB交于点C,与边AB交于点D.
(1)若折叠后使点B与点A重合,求点C的坐标;
(2)若折叠后点B落在边OA上的点为B′,设OB′=x,OC=y,试写出y关于x的函数解析式,并确定y的取值范围;
(3)若折叠后点B落在边OA上的点为B′,且使B′D//OB,求此时点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y=![]() x的图象与反比例函数y=
x的图象与反比例函数y=![]() 的图象交于A(a,-2),B两点.
的图象交于A(a,-2),B两点.
(1)求反比例函数的表达式和点B的坐标;
(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连接PO,若△POC的面积为3,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
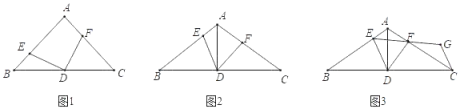
【题目】在△ABC中,AB=AC,点D是BC中点,∠EDF两边分别交线段AB于点E,交线段AC于点F,且∠EDF+∠BAC=180°
(1)如图1,当∠EDF=90°时,求证:BE=AF;
(2)如图2,当∠EDF=60°时,求证:AE+AF=AD;
(3)如图3,在(2)的条件下,连接EF并延长EF至点G,使FG=EF,连接CG,若BE=5,CF=4,求CG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)△ABC满足什么条件时,四边形ADCF是矩形?并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将△ABC纸片沿中位线EH折叠,使点A对称点D落在BC边上,再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF,HG折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.




(1)将□ABCD纸片按图2的方式折叠成一个叠合矩形AEFG,则操作形成的折痕分别是线段_______,_________;S矩形AEFG:S□ABCD=__________.
(2)□ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH,若EF=5,EH=12,求AD的长;
(3)如图4,四边形ABCD纸片满足AD∥BC,AD<BC,AB⊥BC,AB=8,CD=10,小明把该纸片折叠,得到叠合正方形,请你帮助画出一种叠合正方形的示意图,并求出AD、BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
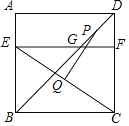
【题目】如图,正方形ABCD的边长为12,点E在边AB上,BE=8,过点E作EF∥BC,分别交BD、CD于G、F两点.若点P、Q分别为DG、CE的中点,则PQ的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
对这30个数据按组距3进行分组,并整理、描述和分析如下.
频数分布表
组别 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
销售额 |
|
|
|
|
|
|
|
频数 | 7 | 9 | 3 |
| 2 |
| 2 |
数据分析表
平均数 | 众数 | 中位数 |
20.3 |
| 18 |
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)若将月销售额不低于25万元确定为销售目标,则有 位营业员获得奖励;
(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是反比例函数y=![]() (x>0)图象上一点,直线y=kx+b过点A并且与两坐标轴分别交于点B,C,过点A作AD⊥x轴,垂足为D,连接DC,若△BOC的面积是4,则△DOC的面积是______.
(x>0)图象上一点,直线y=kx+b过点A并且与两坐标轴分别交于点B,C,过点A作AD⊥x轴,垂足为D,连接DC,若△BOC的面积是4,则△DOC的面积是______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com