
【题目】如图,在平面直角坐标系中,点A、B分别在x轴、y轴上.
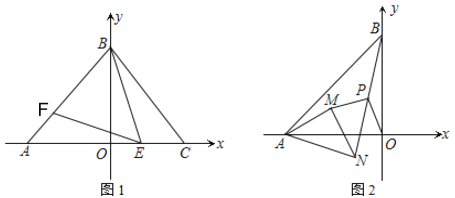
(1)如图1,点A与点C关于y轴对称,点E、F分别是线段AC、AB上的点(点E不与点A、C重合),且∠BEF=∠BAO.若∠BAO=2∠OBE,求证:AF=CE;
(2)如图2,若OA=OB,在点A处有一等腰△AMN绕点A旋转,且AM=MN,∠AMN=90°.连接BN,点P为BN的中点,试猜想OP和MP的数量关系和位置关系,说明理由.
【答案】(1)证明见解析;(2)OP⊥MP且OP=MP,理由见解析.
【解析】
(1)设∠OBE=α,∠AEF=β,证明∠EBC=∠AEF,EB=EF,进而可以证明△AEF和△CBE(AAS),利用全等三角形的对应边相等,即可解答;
(2)OP=MP且OP⊥MP,延长MP至C,且使PC=MP,连接BC、MO,延长AM交BC于D,连接CO,NO,证明△MPN≌△CPB(SAS),得到BC=MN=AM,∠MNP=∠CBP,再证明△MOC为等腰直角三角形,根据MP=CP,即可得到OP⊥MP且OP=MP.
(1)证明:如图1,

设∠OBE=α,∠AEF=β,
∴∠BAO=∠BEF=2α,
∵点A、C关于y轴对称,
∴BA=BC,
∴∠BAO=∠BCO=2α,
∵∠AEB=2α+β=∠BCO+∠EBC,
∴∠EBC=β,
即∠EBC=∠AEF,
∵∠BFE=∠BAO+∠FEA=2α+β,
又∠ABO=∠CBO=α+β,
∴∠FBE=α+β+α=2α+β,
∴∠BFE=∠FBE,
∴EB=EF,
在△AEF和△CBE中,
 ,
,
∴△AEF≌△CBE(AAS)
∴AF=CE;
(2)OP=MP且OP⊥MP,
理由如下:
延长MP至C,且使PC=MP,连接BC、MO,延长AM交BC于D,连接CO,NO,

∵点P为BN的中点,
∴PN=PB,
在△MPN和△CPB中,
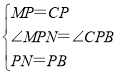 ,
,
∴△MPN≌△CPB(SAS)
∴BC=MN=AM,∠MNP=∠CBP,
∴MN∥BC,
∵∠AMN=90°,
∴AD⊥BC,
∴∠MAO=∠CBO,
∴△MAO≌△CBO(SAS),
∴∠MOA=∠COB,MO=CO,
∴∠MOC=∠MOB+∠BOC=∠MOB+∠MOA=∠AOB=90°,
∴△MOC为等腰直角三角形,
∵MP=CP,
∴OP⊥MP且OP=MP.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.为提前了解学生的选修情况,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行了整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:

(1)本次调查的学生共有 人,在扇形统计图中,m的值是 ;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线1上有A,B两点,AB=12cm,点O是线段AB上的一点,OA=2OB.
(1)OA=______cm,OB=______cm;
(2)若点C是线段AB上一点(点C不与点AB重合),且满足AC=CO+CB,求CO的长;
(3)若动点P,Q分别从A,B同时出发,向右运动,点P的速度为2cm/s,点Q的速度为1cm/s.设运动时间为t(s),当点P与点Q重合时,P,Q两点停止运动.求当t为何值时,2OP-OQ=4(cm);
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知点![]() 及直线
及直线![]() ,根据下列要求画图:
,根据下列要求画图:

(1)作直线![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ;
;
(2)画线段![]() ,并取
,并取![]() 的中点
的中点![]() ,作射线
,作射线![]() ;
;
(3)连接![]() 并延长至点
并延长至点![]() ,使得
,使得![]()
(4)请在直线![]() 上确定一点
上确定一点![]() ,使点
,使点![]() 到点
到点![]() 与点
与点![]() 的距离之和
的距离之和![]() 最小.
最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
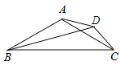
【题目】如图:等腰△ABC中,AB=AC,点D在AC右侧,∠BAC=∠BDC=120°
(1)猜想DA,DC,DB的数量关系并证明
(2)点D 在AB边左侧时三条线段关系是否发生变化?请画出图形。若变化,直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小刚相约周末到雪莲大剧院看演出,他们的家分别距离剧院1200m和2000m,两人分别从家中同时出发,已知小明和小刚的速度比是3:4,结果小明比小刚提前4min到达剧院.求两人的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月23日,是第23个世界读书日.为了推进中华传统文化教育,营造浓厚的读书氛围,我市某学校举办了“让读书成为习惯,让书香溢病校园”主题活动.为了解学生每周阅读时间,该校随机抽取了部分学生进行调查,根据调查结果,将阅诙时间![]() (单位:小时)分成了
(单位:小时)分成了![]() 组,
组, ![]()
![]()
![]() ,下图是根据这组数据绘制的两幅不完整的统计图.请你结合图中所给信息解答下列问题:
,下图是根据这组数据绘制的两幅不完整的统计图.请你结合图中所给信息解答下列问题:
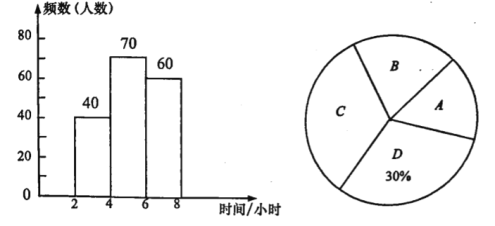
(1)这次随机抽取了 名学生进行调查;
(2)补全频数分布直方图;
(3)计算扇形统计图中扇形![]() 的圆心角的度数;
的圆心角的度数;
(4)若该校共有![]() 名学生,请你估计每周阅读时间不足
名学生,请你估计每周阅读时间不足![]() 小时的学生共有多少名?
小时的学生共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
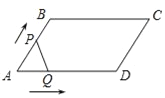
【题目】如图,在平行四边形ABCD中,∠A=60°,AB=6厘米,BC=12厘米,点P、Q同时从 顶点A出发,点P沿A→B→C→D方向以2厘米/秒的速度前进,点Q沿A→D方向以1厘米/秒的速度前进,当Q到达点D时,两个点随之停止运动.设运动时间为x秒,P、Q经过的路径与线段PQ围成的图形的面积为y(cm2),则y与x的函数图象大致是( )
A. 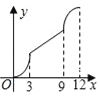 B.
B. 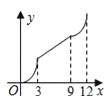 C.
C. 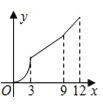 D.
D. 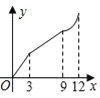
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com