
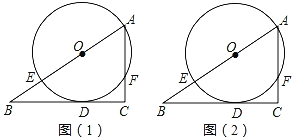
【题目】如图,已知点E在直角三角形ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D.
(1)请仅用无刻度的直尺在图1中作出∠BAC的平分线;
(2)请仅用无刻度的直尺在图2中的线段BC上取一个点P,使CP=EF.
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
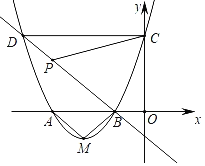
【题目】如图,抛物线y=(x+2)2+m与x轴交于A,B两点,与y轴交于点C.点D在抛物线上,且与点C关于抛物线的对称轴对称,抛物线的顶点为M,点B的坐标为(﹣1,0).
(1)求抛物线的解析式及A,C,D的坐标;
(2)判断△ABM的形状,并证明你的结论;
(3)若点P是直线BD上一个动点,是否存在以P,C,D为顶点的三角形与△ABD相似?若存在,请直接写出点P的坐标;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
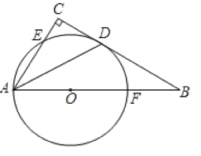
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC、AB于点E. F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2![]() ,BF=2,求⊙O的半径.
,BF=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
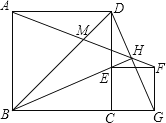
【题目】如图,ABCD、CEFG是正方形,E在CD上,直线BE、DG交于H,且HEHB=4-2![]() ,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=
,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=![]() AM;④若BE平分∠DBC,则正方形ABCD的面积为4,其中结论正确的是______(填序号)
AM;④若BE平分∠DBC,则正方形ABCD的面积为4,其中结论正确的是______(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
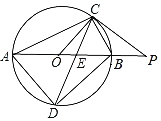
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,连接AC、BC,过点C作∠BCP=∠BAC,交AB的延长线于点P,弦CD平分∠ACB,交AB于点E,连接OC、AD、BD.
(1)求证:PC为⊙O的切线;
(2)若OC=5,OE=1,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某灯饰商店销售一种进价为每件20元的护眼灯.销售过程中发现,每月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的关系可近似地看作一次函数
(元)之间的关系可近似地看作一次函数![]() .物价部门规定该品牌的护眼灯售价不能超过36元.
.物价部门规定该品牌的护眼灯售价不能超过36元.
(1)如果该商店想要每月获得2000元的利润,那么销售单价应定为多少元?
(2)设该商店每月获得利润为![]() (元),当销售单价定为多少元时,每月可获得最大利润?最大利润为多少元?
(元),当销售单价定为多少元时,每月可获得最大利润?最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB中点,AE∥CD,CE∥AB.
(1)试判断四边形ADCE的形状,并证明你的结论.
(2)连接BE,若∠BAC=30°,CE=1,求BE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com