练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，四边形ABCD是菱形，∠A=60°，AB=2，扇形BEF的半径为2，圆心角为60°，则图中阴影部分的面积是（ ）

    A. B. C. D.

    【答案】B

    【解析】试题分析：连接BD，

    ∵四边形ABCD是菱形，∠A=60°，

    ∴∠ADC=120°，

    ∴∠1=∠2=60°，

    ∴△DAB是等边三角形，

    ∵AB=2，

    ∴△ABD的高为，

    ∵扇形BEF的半径为2，圆心角为60°，

    ∴∠4+∠5=60°，∠3+∠5=60°，

    ∴∠3=∠4，

    设AD、BE相交于点G，设BF、DC相交于点H，

    在△ABG和△DBH中，

    ，

    ∴△ABG≌△DBH（ASA），

    ∴四边形GBHD的面积等于△ABD的面积，

    ∴图中阴影部分的面积是：S扇形EBF-S△ABD=

    =．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】用适当方法解下列方程组

    （1） （2）

    （3） （4）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面各问题中给出的两个变量x，y，其中y是x的函数的是

    ① x是正方形的边长，y是这个正方形的面积；

    ② x是矩形的一边长，y是这个矩形的周长；

    ③ x是一个正数，y是这个正数的平方根；

    ④ x是一个正数，y是这个正数的算术平方根．

    A. ①②③B. ①②④C. ②④D. ①④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小学时候大家喜欢玩的幻方游戏，老师稍加创新改成了“幻圆”游戏，现在将﹣1、2、﹣3、4、﹣5、6、﹣7、8分别填入图中的圆圈内，使横、竖以及内外两圈上的4个数字之和都相等，老师已经帮助同学们完成了部分填空，则图中a+b的值为（　　）

    A. ﹣6或﹣3 B. ﹣8或1 C. ﹣1或﹣4 D. 1或﹣1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知抛物线y=x2+bx+c（b，c为常数）的顶点为P，等腰直角三角形ABC的顶点A的坐标为（0，﹣1），C的坐标为（4，3），直角顶点B在第四象限．

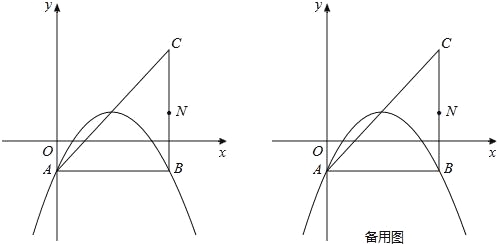
    （1）如图，若该抛物线过A，B两点，求该抛物线的函数表达式；

    （2）平移（1）中的抛物线，使顶点P在直线AC上滑动，且与AC交于另一点Q．

    （i）若点M在直线AC下方，且为平移前（1）中的抛物线上的点，当以M、P、Q三点为顶点的三角形是等腰直角三角形时，求出所有符合条件的点M的坐标；

    （ii）取BC的中点N，连接NP，BQ．试探究是否存在最大值？若存在，求出该最大值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】新学期，两摞观格相同准备发放的数学课本整齐地叠放在讲合上，请根据图中所给出的数据信息，解答下列问题：

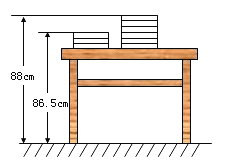
    （1）设课本数（本），请写出整齐叠放在桌面上的数学课本距离地面的高度的代数式（用含的代数式表示）；

    （2）桌面上有56本与题（1）中相同的数学课本，整齐叠放成一摞，若从中取走14本，求余下的数学课本距离地面的高度.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察下面的点阵图形和与之相对应的等式，探究其中的规律：

    （1）请你在④和⑤后面的横线上分别写出相对应的等式：

    ①；

    ②；

    ③；

    ④ _______________；

    ⑤_______________；

    …… ……

    （2）通过猜想，写出与第n个图形相对应的等式：____________________，并说明你猜想的正确性（写出说明过程）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知∠MON=140°，∠AOC与∠BOC互余，OC平分∠MOB，

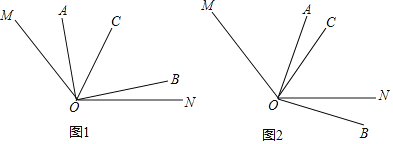
    （1）在图1中，若∠AOC=40°，则∠BOC= °，∠NOB= °．

    （2）在图1中，设∠AOC=α，∠NOB=β，请探究α与β之间的数量关系（ 必须写出推理的主要过程，但每一步后面不必写出理由）；

    （3）在已知条件不变的前提下，当∠AOB绕着点O顺时针转动到如图2的位置，此时α与β之间的数量关系是否还成立？若成立，请说明理由；若不成立，请直接写出此时α与β之间的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知数轴上的点A表示的数为6，点B表示的数为﹣4，点C是AB的中点，动点P从点B出发，以每秒2个单位长度的速度沿数轴向右匀速运动，设运动时间为x秒（x＞0）．

    （1）当x=　 　秒时，点P到达点A；

    （2）运动过程中点P表示的数是　 　（用含x的代数式表示）；

    （3）当P，C之间的距离为2个单位长度时，求x的值．

    查看答案和解析>>

    同步练习册答案