
����Ŀ����ͼ1����֪��MON=140�㣬��AOC���BOC���࣬OCƽ�֡�MOB��
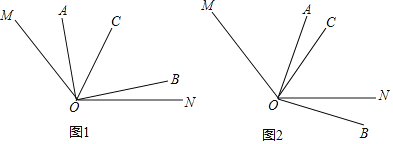
��1����ͼ1�У�����AOC=40�������BOC= �㣬��NOB= �㣮
��2����ͼ1�У����AOC=������NOB=������̽��������֮���������ϵ�� ����д����������Ҫ���̣���ÿһ�����治��д�����ɣ���
��3������֪���������ǰ���£�����AOB���ŵ�O˳ʱ��ת������ͼ2��λ�ã���ʱ������֮���������ϵ�Ƿ���������������˵�����ɣ�������������ֱ��д����ʱ������֮���������ϵ��
���𰸡��⣺��1��50��40����2����=2����40��;��3������������ʱ��ʱ������֮���������ϵΪ��2��+��=40��.
��������
��1���ȸ�����ǵĶ�������BOC=50�������ɽ�ƽ���ߵĶ�������BOM=100�������ݽǵIJ�ɵá�BON�Ķ�����
��2��ͬ���ȼ����MOB=2��BOC=2��90��-����=180��-2�����ٸ��ݡ�BON=��MON-��BOM�е�ʽ���ɣ�
��3��ͬ���ɵá�MOB=180��-2�����ٸ��ݡ�BON+��MON=��BOM�е�ʽ���ɣ�
��1����ͼ1��
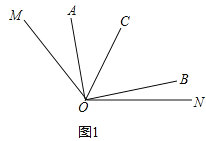
�ߡ�AOC���BOC���࣬
���AOC+��BOC=90����
�ߡ�AOC=40����
���BOC=50����
��OCƽ�֡�MOB��
���MOC=��BOC=50����
���BOM=100����
�ߡ�MON=40����
���BON=��MON-��BOM=140��-100��=40����
��2����=2��-40���������ǣ�
��ͼ1���ߡ�AOC=����
���BOC=90��-����
��OCƽ�֡�MOB��
���MOB=2��BOC=2��90��-����=180��-2����
�֡ߡ�MON=��BOM+��BON��
��140��=180��-2��+��������=2��-40�㣻
��3������������ʱ��ʱ������֮���������ϵΪ��2��+��=40�㣬
�����ǣ���ͼ2��
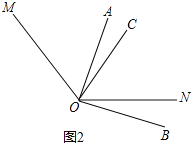
�ߡ�AOC=������NOB=����
���BOC=90��-����
��OCƽ�֡�MOB��
���MOB=2��BOC=2��90��-����=180��-2����
�ߡ�BOM=��MON+��BON��
��180��-2��=140��+������2��+��=40�㣬
�𣺲���������ʱ��ʱ������֮���������ϵΪ��2��+��=40.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͬѧҪ֤�����⡰�Խ�����ȵ�ƽ���ı����Ǿ��Ρ�����ȷ�ģ�������������ͼ��ʾ��ƽ���ı���ABCD����д�������²���������֪����֤��

��֪����ͼ����ƽ���ı���ABCD�У� ��
��֤��ƽ���ı���ABCD�� ��
(1)�ڷ�������գ��Բ�ȫ��֪����֤��
(2)���������뷨д��֤�����̣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�����Σ���A=60����AB=2������BEF�İ뾶Ϊ2��Բ�Ľ�Ϊ60������ͼ����Ӱ���ֵ�����ǣ� ��

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
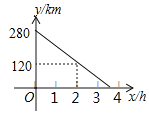
����Ŀ���׳���A��ʻ��B�أ�ͬʱ�ҳ���B��ʻ��A�أ�����������У�������ʻ���׳���B�صľ���y��km������ʻʱ��x��h��֮��ĺ�����ϵ��ͼ��ʾ���ҳ����ٶ���60km/h��
��1����׳����ٶȣ�
��2�������������������ҳ��ٶȱ�Ϊa��km/h����������������ʻ���׳��ٶȱ��ֲ��䣬����ҳ��ȼ׳���38���ӵ����յ㣬��a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
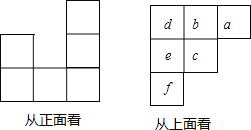
����Ŀ����С�������һ�������壬ʹ������������濴������С�������һ�������壬ʹ������������濴������״��ͼ��ʾ�������濴������״��С�����ε���ĸ��ʾ�ڸ�λ����С������ĸ��������ʣ�
��1��b= ��c= ��
��2����������������� ��С�������ɣ������ ��С�������ɣ�
��3���ܴ�����������ļ����干�м�����������д����濴�ü��������״ͼ���ж�����.�뻭������һ�ִ����濴���ļ��������״ͼ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
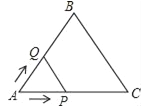
����Ŀ����ͼ���ȱ���ABC�ı߳�Ϊ2cm����P�ӵ�A��������1cm/s���ٶ���AC���C�˶��������Cֹͣ��ͬʱ��Q�ӵ�A��������2cm/s���ٶ���AB��BC���C�˶��������Cֹͣ������APQ�����Ϊy��cm2�����˶�ʱ��Ϊx��s�������������ܷ�ӳy��x֮�亯����ϵ��ͼ������������
A. 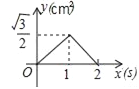 B.
B. 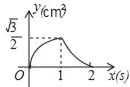
C. 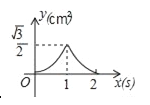 D.
D. 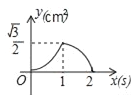
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ��һ���ƽ���һУһ��ӡ�һ��һר�һ��һ���������������������ѧ������Ȥ��������Ŀ��A��������B��������C��������D����ë����E��ƹ�����������ʾ�������ѧ���ɸ����Լ���ϲ��ѡ��һ��������ʦ��ij��ȫ��ͬѧ��ѡ���������ͳ�ƺ����Ƴ���������������ͳ��ͼ����ͼ����
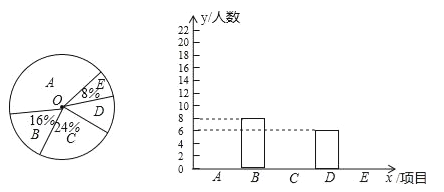
��1���ð��������������Ȥ�������ֱ����� ������ ����
��2������У����ѧ��3500����������ж�����ѡ������
��3���ð��ί5������1��ѡ��������3��ѡ��������1��ѡ������������ʦҪ����5������ѡ2���˽����Ƕ�����ѡ�εĿ������������б�����״ͼ�ķ�������ѡ����2��ǡ��1��ѡ��������1��ѡ������ĸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����߳�Ϊ3����������ABC������ֱ��l�ϣ�AB��ֱ��l�غϣ�������������ABC��ֱ��l�����������Ĺ�������������ABC������һ����ֱ��l�غ�ʱ��¼�������������磬��������ABC��ͼ��λ�âٹ�����λ�â�ʱ��¼Ϊ����һ�Σ�����������ABC��ͼ��λ�âٿ�ʼ����2018��ʱ����A������·���ܳ���Ϊ��������

A.2690��B.2692��C.4034��D.4036��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�����������ʽ��![]() ��
��![]() �������������£����dz�ʹ��ʽ
�������������£����dz�ʹ��ʽ ![]() ������һ��������
������һ��������![]() ��
��![]() ����������������������
����������������������![]() ��
��![]() �����磺���ԣ�
�����磺���ԣ�![]() ��
��![]() ������
������![]() ��
��![]() ��������������������������
��������������������������
��1�����ԣ�![]() ��
��![]() ������
������![]() ��
��![]() ������������������������˵�����ɣ�
������������������������˵�����ɣ�
��2������![]() ��
��![]() ������������������������
������������������������![]() ��
��![]() ����������������������˵�����ɣ�
����������������������˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com