
ЎѕМвДїЎїУГРЎБў·ЅМеґоТ»ёцјёєОМеЈ¬К№ЛьґУХэГжєНЙПГжїґµЅµДУГРЎБў·ЅїйґоТ»ёцјёєОМеЈ¬К№ЛьґУХэГжєНЙПГжїґµЅµДРОЧґИзНјЛщКѕЈ¬ґУЙПГжїґµЅµДРОЧґЦРРЎХэ·ЅРОµДЧЦДё±нКѕФЪёГО»ЦГЙПРЎБў·ЅїйµДёцКэЈ¬ЗлОКЈє
ЈЁ1Ј©b= Ј¬c= Ј»
ЈЁ2Ј©ХвёцјёєОМеЧоЙЩУЙ ёцРЎБў·ЅїйґоіЙЈ¬Чо¶аУЙ ёцРЎБў·ЅїйґоіЙЈ»
ЈЁ3Ј©ДЬґоіцВъЧгМхјюµДјёєОМе№ІУРјёЦЦЗйїцЈїЖдЦРґУЧуГжїґёГјёєОМеµДРОЧґНј№ІУР¶аЙЩЦЦ.Зл»іцЖдЦРТ»ЦЦґУЧуГжїґµЅµДјёєОМеµДРОЧґНјЈ®
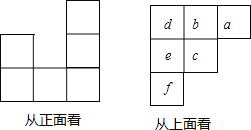

Ўѕґр°ёЎїЈЁ1Ј©1Ј»3Ј»ЈЁ2Ј©9Ј¬11Ј»ЈЁ3Ј©7.
ЎѕЅвОцЎї
ЈЁ1Ј©УЙЦчКУНјїЙЦЄЈ¬µЪ¶юБРРЎБў·ЅМеµДёцКэѕщОЄ1Ј¬µЪ3БРРЎХэ·ЅМеµДёцКэОЄ3Ј¬ДЗГґb=1Ј¬a=3Ј»
ЈЁ2Ј©µЪТ»БРРЎБў·ЅМеµДёцКэЧоЙЩОЄ2+1+1Ј¬ДЗГґјУЙПЖдЛыБЅБРРЎБў·ЅМеµДёцКэјґїЙЈ»
ЈЁ3Ј©УЙЈЁ2Ј©їЙЦЄЈ¬ХвёцјёєОМеЧоЙЩУЙ9ёцРЎБў·ЅїйґоіЙЈ¬УЦµЪТ»БРРЎБў·ЅМеµДёцКэЧо¶аОЄ2+2+2Ј¬ДЗГґЧо¶аУЙ11ёцРЎБў·ЅїйґоіЙЈ¬ЛщТФ№ІУР7ЦЦЗйїцЈ»РЎБў·ЅїйЧо¶аК±јёєОМеµДЧуКУНјУР3БРЈ¬ГїБРРЎХэ·ЅРОКэДї·Ц±рОЄ3Ј¬2Ј¬2Ј®
(1)1Ўў3Ј»
ўЖХвёцјёєОМеЧоЙЩУЙ4+2+3=9ёцРЎБў·ЅїйґоіЙЈ»
ХвёцјёєОМеЧо¶аУЙ6+2+3=11ёцРЎБў·ЅїйґоіЙЈ»
ўЗДЬґоіцВъЧгМхјюµДјёєОМе№ІУР7ЦЦЗйїцЈ¬РЎБў·ЅїйЧо¶аК±јёєОМеµДЧуКУНјИзНјЛщКѕЈє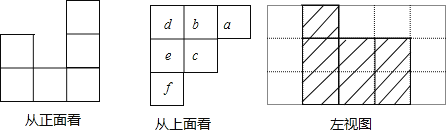
№Кґр°ёОЄ7Ј®



| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ТСЦЄµгCКЗТФABОЄЦ±ѕ¶µДЎСOЙПТ»µгЈ¬CHЎНABУЪµгHЈ¬№эµгBЧчЎСOµДЗРПЯЅ»Ц±ПЯACУЪµгDЈ¬µгEОЄCHµДЦРµгЈ¬Б¬ЅУAEІўСУі¤Ѕ»BDУЪµгFЈ¬Ц±ПЯCFЅ»ABµДСУі¤ПЯУЪGЈ®
ЈЁ1Ј©ЗуЦ¤ЈєAEFD=AFECЈ»
ЈЁ2Ј©ЗуЦ¤ЈєFC=FBЈ»
ЈЁ3Ј©ИфFB=FE=2Ј¬ЗуЎСOµД°лѕ¶rµДі¤Ј®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪЖЅГжЦ±ЅЗЧш±кПµЦРЈ¬ТСЦЄЕЧОпПЯy=![]() x2+bx+cЈЁbЈ¬cОЄіЈКэЈ©µД¶ҐµгОЄPЈ¬µИСьЦ±ЅЗИэЅЗРОABCµД¶ҐµгAµДЧш±кОЄЈЁ0Ј¬©Ѓ1Ј©Ј¬CµДЧш±кОЄЈЁ4Ј¬3Ј©Ј¬Ц±ЅЗ¶ҐµгBФЪµЪЛДПуПЮЈ®
x2+bx+cЈЁbЈ¬cОЄіЈКэЈ©µД¶ҐµгОЄPЈ¬µИСьЦ±ЅЗИэЅЗРОABCµД¶ҐµгAµДЧш±кОЄЈЁ0Ј¬©Ѓ1Ј©Ј¬CµДЧш±кОЄЈЁ4Ј¬3Ј©Ј¬Ц±ЅЗ¶ҐµгBФЪµЪЛДПуПЮЈ®
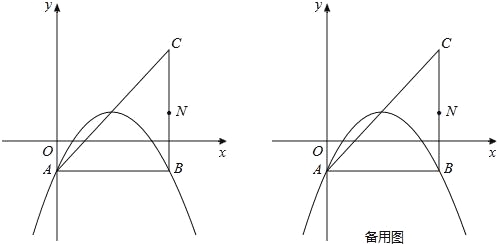
ЈЁ1Ј©ИзНјЈ¬ИфёГЕЧОпПЯ№эAЈ¬BБЅµгЈ¬ЗуёГЕЧОпПЯµДєЇКэ±нґпКЅЈ»
ЈЁ2Ј©ЖЅТЖЈЁ1Ј©ЦРµДЕЧОпПЯЈ¬К№¶ҐµгPФЪЦ±ПЯACЙП»¬¶ЇЈ¬ЗТУлACЅ»УЪБнТ»µгQЈ®
ЈЁiЈ©ИфµгMФЪЦ±ПЯACПВ·ЅЈ¬ЗТОЄЖЅТЖЗ°ЈЁ1Ј©ЦРµДЕЧОпПЯЙПµДµгЈ¬µ±ТФMЎўPЎўQИэµгОЄ¶ҐµгµДИэЅЗРОКЗµИСьЦ±ЅЗИэЅЗРОК±Ј¬ЗуіцЛщУР·ыєПМхјюµДµгMµДЧш±кЈ»
ЈЁiiЈ©ИЎBCµДЦРµгNЈ¬Б¬ЅУNPЈ¬BQЈ®КФМЅѕї![]() КЗ·сґжФЪЧоґуЦµЈїИфґжФЪЈ¬ЗуіцёГЧоґуЦµЈ»ИфІ»ґжФЪЈ¬ЗлЛµГчАнУЙЈ®
КЗ·сґжФЪЧоґуЦµЈїИфґжФЪЈ¬ЗуіцёГЧоґуЦµЈ»ИфІ»ґжФЪЈ¬ЗлЛµГчАнУЙЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎї№ЫІмПВГжµДµгХуНјРОєНУлЦ®Па¶ФУ¦µДµИКЅЈ¬МЅѕїЖдЦРµД№жВЙЈє
ЈЁ1Ј©ЗлДгФЪўЬєНўЭєуГжµДєбПЯЙП·Ц±рРґіцПа¶ФУ¦µДµИКЅЈє
ўЩ![]() Ј»
Ј»
ўЪ![]()
![]() Ј»
Ј»
ўЫ![]()
![]() Ј»
Ј»
ўЬ![]()
![]() _______________Ј»
_______________Ј»
ўЭ
![]() _______________Ј»
_______________Ј»
ЎЎ ЎЎ
ЈЁ2Ј©НЁ№эІВПлЈ¬РґіцУлµЪnёцНјРОПа¶ФУ¦µДµИКЅЈє____________________Ј¬ІўЛµГчДгІВПлµДХэИ·РФЈЁРґіцЛµГч№эіМЈ©Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЙиPЈЁxЈ¬0Ј©КЗxЦбЙПµДТ»ёц¶ЇµгЈ¬ЛьУлФµгµДѕаАлОЄy1Ј®
ЈЁ1Ј©Зуy1№ШУЪxµДєЇКэЅвОцКЅЈ¬Іў»іцХвёцєЇКэµДНјПуЈ»
ЈЁ2Ј©Иф·ґ±ИАэєЇКэy2![]() µДНјПуУлєЇКэy1µДНјПуПаЅ»УЪµгAЈ¬ЗТµгAµДЧЭЧш±кОЄ2Ј®
µДНјПуУлєЇКэy1µДНјПуПаЅ»УЪµгAЈ¬ЗТµгAµДЧЭЧш±кОЄ2Ј®
ўЩЗуkµДЦµЈ»
ўЪЅбєПНјП󣬵±y1Јѕy2К±Ј¬РґіцxµДИЎЦµ·¶О§Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНј1Ј¬ТСЦЄЎПMON=140ЎгЈ¬ЎПAOCУлЎПBOC»ҐУаЈ¬OCЖЅ·ЦЎПMOBЈ¬
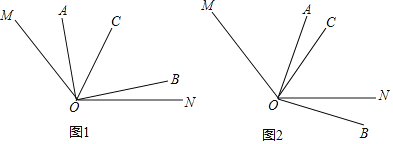
ЈЁ1Ј©ФЪНј1ЦРЈ¬ИфЎПAOC=40ЎгЈ¬ФтЎПBOC= ЎгЈ¬ЎПNOB= ЎгЈ®
ЈЁ2Ј©ФЪНј1ЦРЈ¬ЙиЎПAOC=¦БЈ¬ЎПNOB=¦ВЈ¬ЗлМЅѕї¦БУл¦ВЦ®јдµДКэБї№ШПµЈЁ ±ШРлРґіцНЖАнµДЦчТЄ№эіМЈ¬µ«ГїТ»ІЅєуГжІ»±ШРґіцАнУЙЈ©Ј»
ЈЁ3Ј©ФЪТСЦЄМхјюІ»±дµДЗ°МбПВЈ¬µ±ЎПAOBИЖЧЕµгOЛіК±ХлЧЄ¶ЇµЅИзНј2µДО»ЦГЈ¬ґЛК±¦БУл¦ВЦ®јдµДКэБї№ШПµКЗ·с»№іЙБўЈїИфіЙБўЈ¬ЗлЛµГчАнУЙЈ»ИфІ»іЙБўЈ¬ЗлЦ±ЅУРґіцґЛК±¦БУл¦ВЦ®јдµДКэБї№ШПµЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
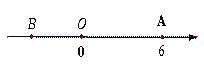
ЎѕМвДїЎїИзНјЈ¬ТСЦЄКэЦбЙПµДµгA¶ФУ¦µДКэОЄ6Ј¬BКЗКэЦбЙПµДТ»µгЈ¬ЗТAB=10Ј¬¶ЇµгPґУµгAіц·ўЈ¬ТФГїГл6ёцµҐО»і¤¶ИµДЛЩ¶ИСШЧЕКэЦбПтЧуФИЛЩФЛ¶ЇЈ¬ЙиФЛ¶ЇК±јдОЄtГл(t>0).
(1)КэЦбЙПµгB¶ФУ¦µДКэКЗ_______Ј¬µгP¶ФУ¦µДКэКЗ_______(УГtµДКЅЧУ±нКѕ)Ј»
(2)¶ЇµгQґУµгBУлµгPН¬К±іц·ўЈ¬ТФГїГл4ёцµҐО»і¤¶ИµДЛЩ¶ИСШЧЕКэЦбПтЧуФИЛЩФЛ¶ЇЈ¬КФОКЈєФЛ¶Ї¶аЙЩК±јдµгPїЙТФЧ·ЙПµгQЈї
(3)MКЗAPµДЦРµгЈ¬NКЗPBµДЦРµгЈ¬µгPФЪФЛ¶Ї№эіМЦРЈ¬ПЯ¶ОMNµДі¤¶ИКЗ·с·ўЙъ±д»ЇЈїИфУР±д»ЇЈ¬ЛµГчАнУЙЈ»ИфГ»УР±д»ЇЈ¬ЗлДг»іцНјРОЈ¬ІўЗуіцMNµДі¤.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
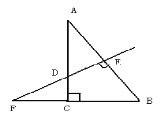
ЎѕМвДїЎїИзНјЈ¬RtЎчABCЦРЈ¬ЎПACB=90ЎгЈ¬ABµДґ№Ц±ЖЅ·ЦПЯDEЅ»BCµДСУі¤ПЯУЪFЈ¬ИфЎПF=30ЎгЈ¬DE=1,ФтEFµДі¤КЗ_____.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїДіµчІй»ъ№№Ѕ«ЅсДкОВЦЭКРГсЧо№ШЧўµДИИµг»°Мв·ЦОЄПы·СЎўЅМУэЎў»·±ЈЎў·ґёЇј°ЖдЛь№ІОеАаЈ®ёщѕЭЧоЅьТ»ґОЛж»ъµчІйµДПа№ШКэѕЭЈ¬»жЦЖµДНіјЖНј±нИзПВЈє
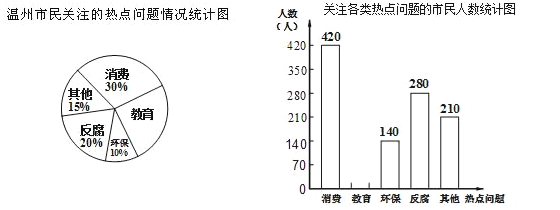
ёщѕЭТФЙПРЕПўЅвґрПВБРОКМвЈє
ЈЁ1Ј©±ѕґО№ІµчІйЎЎ ЎЎИЛЈ¬ЗлФЪґрМвїЁЙПІ№И«МхРОНіјЖНјІў±кіцПаУ¦КэѕЭЈ»
ЈЁ2Ј©ИфОВЦЭКРФјУР900НтИЛїЪЈ¬ЗлДг№АјЖЧо№ШЧўЅМУэОКМвµДИЛКэФјОЄ¶аЙЩНтИЛЈї
ЈЁ3Ј©ФЪХвґОµчІйЦРЈ¬ДіµҐО»№ІУРјЧЎўТТЎў±ыЎў¶ЎЛДИЛЧо№ШЧўЅМУэОКМвЈ¬ПЦЧј±ёґУХвЛДИЛЦРЛж»ъійИЎБЅИЛЅшРРЧщМёЈ¬ЗуійИЎµДБЅИЛЗЎєГКЗјЧєНТТµДёЕВКЈЁБРКэЧґНј»тБР±нЛµГчЈ©Ј®
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com