
【题目】观察下面的点阵图形和与之相对应的等式,探究其中的规律:
(1)请你在④和⑤后面的横线上分别写出相对应的等式:
①![]() ;
;
②![]()
![]() ;
;
③![]()
![]() ;
;
④![]()
![]() _______________;
_______________;
⑤
![]() _______________;
_______________;
…… ……
(2)通过猜想,写出与第n个图形相对应的等式:____________________,并说明你猜想的正确性(写出说明过程).
【答案】(1)4×3+1=4×4-3;4×4+1=4×5-3;(2)4(n-1)+1=4n-3.
【解析】
(1)结合图形,根据所给等式即可继续写出下面的等式;(2)根据上述等式,推而广之,与第n个图形相对应的等式是4(n-1)+1=4n-3.
(1)根据前三个式子可知:④中是4×3+1=4×4-3;⑤中是4×4+1=4×5-3,
故答案为:4×3+1=4×4-3;4×4+1=4×5-3
(2)∵0=1-1,1=2-1,2=3-1,……,
∴猜想第n个图形相对应的等式为:4(n-1)+1=4n-3.
∵左边=4(n-1)+1=4n-4+1=4n-3,右边=4n-3,
∴左边=右边,
∴等式成立.
故答案为:4(n-1)+1=4n-3


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AB=CD,BC=10,对角线AC、BD相交于点O,且AC⊥BD,设AD=x,△AOB的面积为y.
(1)求∠DBC的度数;
(2)求y关于x的函数解析式,并写出自变量x的取值范围;
(3)如图1,设点P、Q分别是边BC、AB的中点,分别联结OP,OQ,PQ.如果△OPQ是等腰三角形,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了庆祝新中国成立70周年,某校组织八年级全体学生参加“恰同学少年,忆峥嵘岁月”新中国成立70周年知识竞赛活动.将随机抽取的部分学生成绩进行整理后分成5组,50~60分(![]() )的小组称为“学童”组,60~70分(
)的小组称为“学童”组,60~70分(![]() )的小组称为“秀才”组,70~80分(
)的小组称为“秀才”组,70~80分(![]() )的小组称为“举人”组,80~90分(
)的小组称为“举人”组,80~90分(![]() )的小组称为“进士”组,90~100分(
)的小组称为“进士”组,90~100分(![]() )的小组称为“翰林”组,并绘制了不完整的频数分布直方图如下,请结合提供的信息解答下列问题:
)的小组称为“翰林”组,并绘制了不完整的频数分布直方图如下,请结合提供的信息解答下列问题:
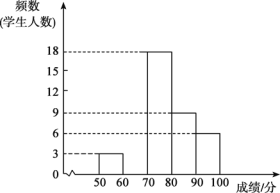
(1)若“翰林”组成绩的频率是12.5%,请补全频数分布直方图;
(2)在此次比赛中,抽取学生的成绩的中位数在 组;
(3)学校决定对成绩在70~100分(![]() )的学生进行奖励,若八年级共有336名学生,请通过计算说明,大约有多少名学生获奖?
)的学生进行奖励,若八年级共有336名学生,请通过计算说明,大约有多少名学生获奖?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
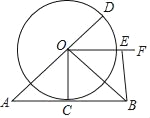
【题目】如图,在△ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C,连接OC,AO延长线交⊙O于点D,OF是∠DOB的平分线,E为OF上一点,连接BE.
(1)求证:AB与⊙O相切;
(2)①当∠OEB=_____时,四边形OCBE为矩形;
②在①的条件下,若AB=4,则OA=_____时,四边形OCBE为正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
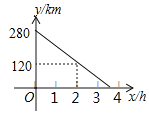
【题目】甲车从A地驶往B地,同时乙车从B地驶往A地,两车相向而行,匀速行驶,甲车距B地的距离y(km)与行驶时间x(h)之间的函数关系如图所示,乙车的速度是60km/h.
(1)求甲车的速度;
(2)当甲乙两车相遇后,乙车速度变为a(km/h),并保持匀速行驶,甲车速度保持不变,结果乙车比甲车晚38分钟到达终点,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
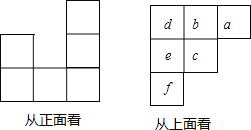
【题目】用小立方体搭一个几何体,使它从正面和上面看到的用小立方块搭一个几何体,使它从正面和上面看到的形状如图所示,从上面看到的形状中小正方形的字母表示在该位置上小立方块的个数,请问:
(1)b= ,c= ;
(2)这个几何体最少由 个小立方块搭成,最多由 个小立方块搭成;
(3)能搭出满足条件的几何体共有几种情况?其中从左面看该几何体的形状图共有多少种.请画出其中一种从左面看到的几何体的形状图.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为进一步推进“一校一球队、一级一专项、一人一技能”的体育活动,决定对学生感兴趣的球类项目(A:足球,B:篮球,C:排球,D:羽毛球,E:乒乓球)进行问卷调查,学生可根据自己的喜好选修一门,李老师对某班全班同学的选课情况进行统计后,制成了两幅不完整的统计图(如图).
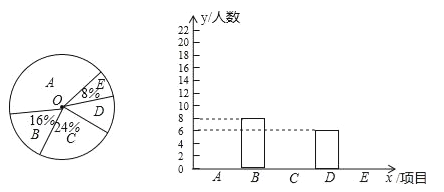
(1)该班对足球和排球感兴趣的人数分别是 、 ;
(2)若该校共有学生3500名,请估计有多少人选修足球?
(3)该班班委5人中,1人选修篮球,3人选修足球,1人选修排球,李老师要从这5人中任选2人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求选出的2人恰好1人选修篮球,1人选修足球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口的直径 EF 长为10cm,母线OE(OF)长为10cm,在母线OF 上的点A 处有一块爆米花残渣且FA=2cm,一只蚂蚁从杯口的点E 处沿圆锥表面爬行到A 点,则此蚂蚁爬行的最短距离为 cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com