
【题目】当a取什么整数时,方程![]() +
+![]() +
+![]() =0只有一个实根,并求此实根.
=0只有一个实根,并求此实根.
【答案】a=﹣4时,原方程恰有一个实根x=1;a=﹣8时,原方程恰有一个实根x=﹣1
【解析】
先将原方程化为![]() =0,再分三种情况进行讨论:
=0,再分三种情况进行讨论:
(1)若x≠0且x≠2,则2x2﹣2x+4+a=0,由原分式方程恰有一个实根,得出△=(﹣2)2﹣4×2×(4+a)=﹣28﹣8a=0,依此求出a的值;
(2)若方程2x2﹣2x+4+a=0,有一个根为x=0,代入求出a=﹣4,再解方程即可;
(3)若方程2x2﹣2x+4+a=0,有一个根为x=2,代入求出a=﹣8,再解方程即可.
解:原方程化为![]() =0.
=0.
(1)若x≠0且x≠2,则2x2﹣2x+4+a=0,
∵原分式方程恰有一个实根,
∴△=0,即△=(﹣2)2﹣4×2×(4+a)=﹣28﹣8a=0,
则a=﹣![]() ,
,
于是x1=x2=![]() ,
,
但a取整数,则舍去;
(2)若方程2x2﹣2x+4+a=0,有一个根为x=0,则a=﹣4,
这时原方程为![]() ,
,
去分母得2x2﹣2x=0,
解得x=0,x=1,
显然x=0是增根,x=1是原分式方程的根;
(3)若方程2x2﹣2x+4+a=0,有一个根为x=2,则a=﹣8,
这时,原方程为![]()
去分母,得2x2﹣2x﹣4=0,
解得x=2,x=﹣1,
显然x=2是增根,x=﹣1是原分式方程的根;
经检验当a=﹣4时,原方程恰有一个实根x=1;当a=﹣8时,原方程恰有一个实根x=﹣1.


科目:初中数学 来源: 题型:
【题目】已知,如图一张三角形纸片ABC,边AB长为10cm,AB边上的高为15cm,在三角形内从左到右叠放边长为2的正方形小纸片,第一次小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放的正方形的个数是( ).
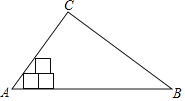
A. 12B. 13C. 14D. 15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E在直角三角形ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D.
(1)请仅用无刻度的直尺在图1中作出∠BAC的平分线;
(2)请仅用无刻度的直尺在图2中的线段BC上取一个点P,使CP=EF.
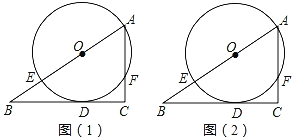
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() 中,
中,![]() ,P是斜边AC上一个动点,以即为直径作
,P是斜边AC上一个动点,以即为直径作![]() 交BC于点D,与AC的另一个交点E,连接DE.
交BC于点D,与AC的另一个交点E,连接DE.
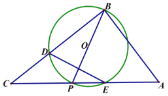
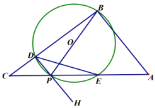
(1)当![]() 时,
时,
①若![]() ,求
,求![]() 的度数;
的度数;
②求证![]() ;
;
(2)当![]() ,
,![]() 时,
时,
①是含存在点P,使得![]() 是等腰三角形,若存在求出所有符合条件的CP的长;
是等腰三角形,若存在求出所有符合条件的CP的长;
②以D为端点过P作射线DH,作点O关于DE的对称点Q恰好落在![]() 内,则CP的取值范围为________.(直接写出结果)
内,则CP的取值范围为________.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c经过直线y=﹣x+3与坐标轴的两个交点A、B,与x轴的另一个交点为C,顶点为D.
(1)求抛物线的解析式;
(2)画出抛物线的图象;
(3)在x轴上是否存在点N使△ADN为直角三角形?若存在,求出点N的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
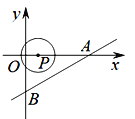
【题目】如图,直线![]() 交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是______________.
交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进某种商品时的单价是40元,根据市场调查:在一段时间内,销售单价是60元时,销售量是300件,而销售单价每涨1元,就会少售出10件.
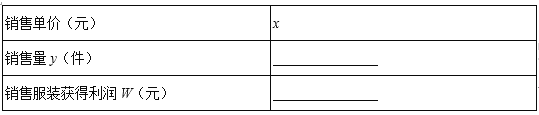
(1)设该种商品的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润W元,并把结果填写在表格中:
(2)在(1)的条件下,若商场获得了4000元销售利润,求该商品销售单价x应定为多少元?
(3)当定价多少时,该商场获得的最大利润,最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com