
【题目】我们把经过原点,顶点落在同一抛物线C上的所有抛物线称为抛物线C的派生抛物线.
(1)若y1=﹣x2+4x是抛物线C:y=ax2+2的派生抛物线,求a的值.
(2)证明:经过原点的抛物线y=﹣mx2+2mx+m﹣2是抛物线C:y=![]() x2+
x2+![]() 的派生抛物线;
的派生抛物线;
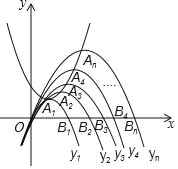
(3)如图,抛物线y1,y2,y3,y4…yn都是抛物线C:y=x2﹣2x+2的派生抛物线,其顶点A1,A2,A3,A4…An的横坐标分别是1、2、3、4…n,它们与x轴的另一个交点分别是B1,B2,B3,B4…Bn,与原点O构成的三角形分别为△OA1B1,△OA2B2,△OA3B3,△OA4B4…△OAnBn.
①请用含n的代数式表示抛物线yn的函数表达式;
②在这些三角形中,是否存在两个相似的三角形,若存在,请直接写出它们所对应的两个函数的表达式,若不存在,请说明理由.
【答案】(1)a=![]() ;(2)见解析;(3)①yn=﹣
;(2)见解析;(3)①yn=﹣![]() (x﹣n)2+n2﹣2n+2,②存在.y1=﹣(x﹣1)2+1,y2=﹣(x﹣2)2+2,理由见解析.
(x﹣n)2+n2﹣2n+2,②存在.y1=﹣(x﹣1)2+1,y2=﹣(x﹣2)2+2,理由见解析.
【解析】
(1)根据派生抛物线的定义构建方程求出a即可;
(2)根据派生抛物线的定义证明即可;
(3)①设yn=a(x-n)2+n2-2n+2,因为经过原点,可得0=a(0-n)2+n2-2n+2,推出a=![]()
②存在.y1=-(x-1)2+1,y2=-(x-2)2+2,理由:△OA1B1,△OA2B2都是等腰直角三角形;
(1)y1=﹣x2+4x的顶点坐标(2,4),
∵y1=﹣x2+4x是抛物线C:y=ax2+2的派生抛物线,
∴4=4a+2,
∴![]()
(2)∵抛物线经过原点(0,0),
∴m﹣2=0,
∴m=2,
∴抛物线的解析式为y=﹣2x2+4x,顶点(1,2),
当x=1时,![]()
∴抛物线的解析式为y=﹣2x2+4x,顶点(1,2)在抛物线C:![]()
∴经过原点的抛物线y=﹣mx2+2mx+m﹣2是抛物线C:![]()
(3)①设yn=a(x﹣n)2+n2﹣2n+2,
∵经过原点,
∴0=a(0﹣n)2+n2﹣2n+2,
∴a=![]()
∴yn=﹣![]()
②存在.y1=﹣(x﹣1)2+1,y2=﹣(x﹣2)2+2,
理由:△OA1B1,△OA2B2都是等腰直角三角形.
∴△OA1B1∽△OA2B2.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
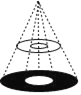
【题目】圆桌面(桌面中间有一个直径为1m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为2m,桌面离地面1m,若灯泡离地面2m,则地面圆环形阴影的面积是( )
A. 2πm2 B. 3πm2 C. 6πm2 D. 12πm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】韦达定理:若一元二次方程ax2+bx+c=0(a≠0)的两根分别为x1、x2 , 则x1+x2=﹣![]() , x1x2=
, x1x2=![]() , 阅读下面应用韦达定理的过程:
, 阅读下面应用韦达定理的过程:
若一元二次方程﹣2x2+4x+1=0的两根分别为x1、x2 , 求x12+x22的值.
解:该一元二次方程的△=b2﹣4ac=42﹣4×(﹣2)×1=24>0
由韦达定理可得,x1+x2=﹣![]() =﹣
=﹣![]() =2,x1x2=
=2,x1x2=![]() =
=![]() =﹣
=﹣![]()
x12+x22=(x1+x2)2﹣2x1x2
=22﹣2×(﹣![]() )
)
=5
然后解答下列问题:
(1)设一元二次方程2x2+3x﹣1=0的两根分别为x1,x2, 不解方程,求x12+x22的值;
(2)若关于x的一元二次方程(k﹣1)x2+(k2﹣1)x+(k﹣1)2=0的两根分别为α,β,且α2+β2=4,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
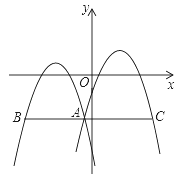
【题目】如图,在平面直角坐标系中,抛物线y=m(x+3)2+n与y=m(x﹣2)2+n+1交于点A.过点A作x轴的平行线,分别交两条抛物线于点B、C(点B在点C左侧),则线段BC的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个箱子里放有1个白球和2个红球,它们除颜色外其余都相同.
(1)从箱子里摸出1个球,是黑球,这属于什么事件;(填“必然”、“不可能”或“随机”)
(2)从箱子里摸出1个球,放回,摇匀后再摸出一个球,请利用树状图或表格计算,这样先后摸得的两个球都是红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
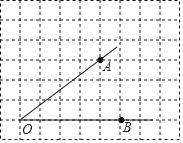
【题目】如图,已知方格纸中的每个小方格都是相同的正方形(边长为1),方格纸上有一个角∠AOB,A,O,B均为格点,请回答问题并只用无刻度直尺和铅笔,完成下列作图并简要说明画法:
(1)OA=_____;
(2)作出∠AOB的平分线并在其上标出一个点Q,使OQ=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=100°,则∠C的度数为( )
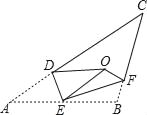
A. 40° B. 41° C. 42° D. 43°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.
(1)求抛物线的表达式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)若抛物线上有一动点M,使△ABM的面积等于△ABC的面积,求M点坐标.
(4)抛物线的对称轴上是否存在动点Q,使得△BCQ为等腰三角形?若存在,求出点Q的坐标;若不存在,说明理由.
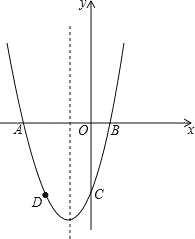
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com