
【题目】韦达定理:若一元二次方程ax2+bx+c=0(a≠0)的两根分别为x1、x2 , 则x1+x2=﹣![]() , x1x2=
, x1x2=![]() , 阅读下面应用韦达定理的过程:
, 阅读下面应用韦达定理的过程:
若一元二次方程﹣2x2+4x+1=0的两根分别为x1、x2 , 求x12+x22的值.
解:该一元二次方程的△=b2﹣4ac=42﹣4×(﹣2)×1=24>0
由韦达定理可得,x1+x2=﹣![]() =﹣
=﹣![]() =2,x1x2=
=2,x1x2=![]() =
=![]() =﹣
=﹣![]()
x12+x22=(x1+x2)2﹣2x1x2
=22﹣2×(﹣![]() )
)
=5
然后解答下列问题:
(1)设一元二次方程2x2+3x﹣1=0的两根分别为x1,x2, 不解方程,求x12+x22的值;
(2)若关于x的一元二次方程(k﹣1)x2+(k2﹣1)x+(k﹣1)2=0的两根分别为α,β,且α2+β2=4,求k的值.
【答案】(1)x12+x22=![]() ;(2)k的值为﹣1.
;(2)k的值为﹣1.
【解析】
(1)先根据根与系数的关系得到x1+x2=﹣![]() , x1x2=﹣
, x1x2=﹣![]() ,再利用完全平方公式变形得到x12+x22=(x1+x2)2-2x1x2,然后利用整体代入的方法计算即可;
,再利用完全平方公式变形得到x12+x22=(x1+x2)2-2x1x2,然后利用整体代入的方法计算即可;
(2)根据一元二次方程(k-1)x2+(k2-1)x+(k-1)2=0的两根分别为α,β,求出两根之积和两根之和的关于k的表达式,再将α2+β2=4变形,将表达式代入变形后的等式,解方程即可.
解:(1)∵一元二次方程的△=b2﹣4ac=32﹣4×2×(﹣1)=17>0,
由根与系数的关系得:x1+x2=﹣![]() , x1x2=﹣
, x1x2=﹣![]() ,
,
∴x12+x22=(x1+x2)2﹣2x1x2=![]() =
=![]() ;
;
(2)由根与系数的关系知:![]() =﹣k﹣1,
=﹣k﹣1,![]() =k﹣1,
=k﹣1,
α2+β2=(α+β)2﹣2αβ=(k+1)2﹣2(k﹣1)=k2+3
∴k2+3=4,
∴k=±1,
∵k﹣1≠0
∴k≠1,
∴![]()
将![]() 代入原方程:﹣2x2+4=0,
代入原方程:﹣2x2+4=0,
△=32>0,
∴![]() 成立,
成立,
∴k的值为![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
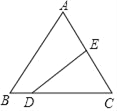
【题目】如图,等边△ABC的边长为8,D、E两点分别从顶点B、C出发,沿边BC、CA以1个单位/s、2个单位/s的速度向顶点C、A运动,DE的垂直平分线交BC边于F点,若某时刻tan∠CDE=![]() 时,则线段CF的长度为_____.
时,则线段CF的长度为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一辆吊车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为3.4m.当起重臂AC长度为9m,张角∠HAC为118°时,求操作平台C离地面的高度(结果保留小数点后一位:参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+3上的三点,则y1,y2,y3的大小关系为( )
A. y1>y2>y3 B. y1>y3>y2 C. y3>y2>y1 D. y3>y1>y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划在总费用2300元的限额内,租用客车送234名学生和6名教师集体外出活动,每辆客车上至少要有1名教师.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 45 | 30 |
租金/(元/辆) | 400 | 280 |
(1)共需租多少辆客车?
(2)请给出最节省费用的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用条长40厘米的绳子围成一个矩形,设其一边长为x厘米.
(1)若矩形的面积为96平方厘米,求x的值;
(2)矩形的面积是否可以为101平方厘米?如果能,请求x的值;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
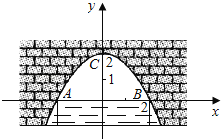
【题目】图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系:
(1)求拱桥所在抛物线的解析式;
(2)当水面下降1m时,则水面的宽度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把经过原点,顶点落在同一抛物线C上的所有抛物线称为抛物线C的派生抛物线.
(1)若y1=﹣x2+4x是抛物线C:y=ax2+2的派生抛物线,求a的值.
(2)证明:经过原点的抛物线y=﹣mx2+2mx+m﹣2是抛物线C:y=![]() x2+
x2+![]() 的派生抛物线;
的派生抛物线;
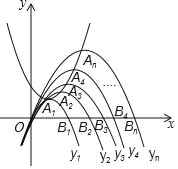
(3)如图,抛物线y1,y2,y3,y4…yn都是抛物线C:y=x2﹣2x+2的派生抛物线,其顶点A1,A2,A3,A4…An的横坐标分别是1、2、3、4…n,它们与x轴的另一个交点分别是B1,B2,B3,B4…Bn,与原点O构成的三角形分别为△OA1B1,△OA2B2,△OA3B3,△OA4B4…△OAnBn.
①请用含n的代数式表示抛物线yn的函数表达式;
②在这些三角形中,是否存在两个相似的三角形,若存在,请直接写出它们所对应的两个函数的表达式,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数的图象经过A(4,0),B(0,﹣4),C(2,﹣4)三点.
(1)求这个函数的解析式;
(2)求函数图顶点的坐标;
(3)求抛物线与坐标轴的交点围成的三角形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com