
已知二次函数的顶点坐标为(2,-2),且其图象经过点(3,1),求此二次函数的解析式,并求出该函数图像与y轴的交点坐标。
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
已知点P(1,-2a)在二次函数y=ax2+6的图象上,并且点P关于x轴的对称点在反比例函数 的图象上。
的图象上。
(1)求此二次函数和反比例函数的解析式;
(2)点(-1,4)是否同时在(1)中的两个函数图象上?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
二次函数y=ax2+c (a≠0)的图象经过点A(1,-1),B(2,5),
(1)求函数y=ax2+c的表达式。
(2)若点C(-2,m),D(n ,7)也在函数的图象上,求点C的坐标;点D的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB.OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.
【小题1】求A、B、C三点的坐标;
【小题2】求此抛物线的表达式
【小题3】连接AC、BC,若点E是线段AB上的一个动点(与点A.点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
【小题4】在(3)的基础上试说明S是否存在最大值,若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
(本题满分8分)九(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
| 甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| 乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
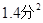 ,则成绩较为整齐的是 队.
,则成绩较为整齐的是 队.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com