
����Ŀ����ͼ�٣���ƽ��ֱ�������У���A������Ϊ��1����2������B������Ϊ��3����1�������κ���y=��x2��ͼ��Ϊl1 �� 
��1��ƽ��������l1 �� ʹƽ�ƺ�������߾�����A����������B��
������������ĺ�������ʽ������
��д������ƽ���Ҿ���A�Ľ���ʽ ��
��2��ƽ��������l1 �� ʹƽ�ƺ�������߾���A��B���㣬���õ�������l2 �� ��ͼ�ڣ���������l2�ĺ�������ʽ������C�����꣬�����ABC�������
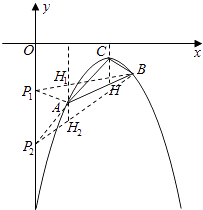
��3����y�����Ƿ���ڵ�P��ʹS��ABC=S��ABP�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��������y=��x2��1
��2��
�⣺��l2�Ľ���ʽ��y=��x2+bx+c��
��l2������A��1����2����B��3����1����
��������ã� ![]() ��
��
��ã� 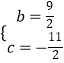 ��
��
��l2�Ľ���ʽ�ǣ�y=��x2+ ![]() x��
x�� ![]() ��
��
��C�������ǣ� ![]() ����
���� ![]() ����
����
����A��B��C����ֱ���x��Ĵ��ߣ�����ֱ�ΪD��E��F����AD=2��CF= ![]() ��BE=1��DE=2��DF=
��BE=1��DE=2��DF= ![]() ��FE=
��FE= ![]() ��
��
�ã�S��ABC=S����ABED��S����BCFE��S����ACFD= ![]()
��������
��l2�Ľ���ʽΪ��y=��x2+bx+c��
��l2������A��1����2����B��3����1����
��������ã� ![]() ��
��
��b= ![]() ��c=��
��c=�� ![]() ��
��
��l2�Ľ���ʽ�ǣ�y=��x2+ ![]() x��
x�� ![]() ��
��
��C�� ![]() ����
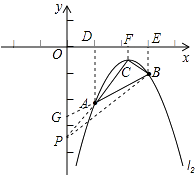
���� ![]() ������O����x��Ĵ��߽�AB��H��
������O����x��Ĵ��߽�AB��H��
��A��1����2����B��3����1����
��lAB��y= ![]() x��
x�� ![]() ����x=
����x= ![]() ���룬y=��
���룬y=�� ![]() ��
��
��H�� ![]() ����
���� ![]() ����
����
��S��ABC= ![]() =
= ![]()
��3��
�⣺�ӳ�BA��y���ڵ�G��ֱ��AB�Ľ���ʽΪy= ![]() x��
x�� ![]() �����G��������0����
�����G��������0���� ![]() �������P��������0��h��
�������P��������0��h��
�ٵ���Pλ�ڵ�G���·�ʱ��PG=�� ![]() ��h������AP��BP����S��APG=S��BPG��S��ABP=����
��h������AP��BP����S��APG=S��BPG��S��ABP=���� ![]() ��h��/2��
��h��/2��
��S��ABP=���� ![]() ��h��
��h��
�֡�S��ABC=S��ABP= ![]() ����h=��
����h=�� ![]() ����P��������0����
����P��������0���� ![]() ����
����
�ڵ���Pλ�ڵ�G���Ϸ�ʱ��PG= ![]() +h��ͬ����h=��
+h��ͬ����h=�� ![]() ����P������Ϊ��0����
����P��������0���� ![]() ����
����
�������������P��������0���� ![]() ����0����
����0���� ![]() ��
��
��������
ֱ��AB��y��Ľ���ΪD��
��lAB��y= ![]() x��
x�� ![]() ����D��0����
����D��0���� ![]() ����
����
��P��0��t����
��S��ABP= ![]() ��
��
�� ![]() ��
��
��t1=�� ![]() ��t2=��
��t2=�� ![]() ��
��
���P��������0���� ![]() ����0����
����0���� ![]() ����
����
���������⣺��1��������������ĺ�������ʽ����������
����ƽ���Ժ�Ķ��κ�������ʽ�ǣ�y=��x2+c����A��1����2������ã���1+c=��2��
��ã�c=��1��
�����Ľ���ʽ�ǣ�y=��x2��1��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������и���
��1�����㣺����2��2�� ![]() ��1+tan45�㣩
��1+tan45�㣩
��2���Ȼ�������ֵ�� ![]() ������a=
������a= ![]() ��2��b=
��2��b= ![]() +2��
+2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC��AD=5cm��BC=9cm��M��CD���е㣬P��BC���ϵ�һ���㣨P��B��C���غϣ�������PM���ӳ���AD���ӳ�����Q�� 
��1����˵����PCM�ա�QDM��
��2������P�ڵ�B��C֮���˶���ʲôλ��ʱ���ı���ABPQ��ƽ���ı��Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽����
��ͼ1���ȱߡ�ABC�У�BC=4����P�ӵ�B��������BC�����˶�����C����P����ֱ��AB��AC�ĶԳƵ�ֱ�Ϊ��M��N������MN��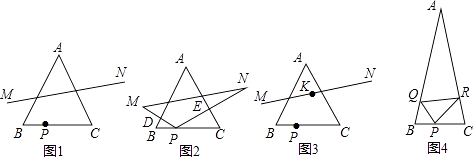
��1�������֡�
����P���B�غ�ʱ���߶�MN�ij��� ��
��AP�ij���Сʱ���߶�MN�ij�����
��2����̽����
��ͼ2����PB=x��MN2=y������PM��PN���ֱ�AB��AC�ڵ�D��E��
�ú�x�Ĵ���ʽ��ʾPM= �� PN=��
��3����y����x�ĺ�����ϵʽ����д��y��ȡֵ��Χ��
��4������P��ֱ��BC�ϵ�ʲôλ��ʱ���߶�MN=3 ![]() ��ֱ��д���𰸣�
��ֱ��д���𰸣�
��5������չ��
��ͼ3�����߶�MN���е�K������·�߳���
��6����Ӧ�á�
��ͼ4���ڵ�����ABC�У���BAC=30�㣬AB=AC��BC=2����P��Q��R�ֱ�Ϊ��BC��AB��AC�ϣ�������˵��غϣ��Ķ��㣬���PQR�ܳ�����Сֵ�� ��
�������õ�����ֵ��sin75��= ![]() ��cos75��=
��cos75��= ![]() ��tan75��=2+
��tan75��=2+ ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ž���ֽƬ������ͼ������ ����ABE��BE���ۣ�ʹ��A���ڶԽ���BD�ϵ�M�㣬����CDF��DF���ۣ�ʹ��C���ڶԽ���BD�ϵ�N�㣮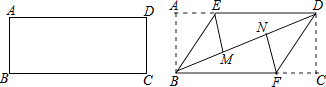
��1����֤���ı���BFDE��ƽ���ı��Σ�
��2�����ı���BFDE�����Σ�AB=2��������BFDE�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽��п�������Ŀѵ�������ij�شӾ��꼶ѧ���������ȡ�˲���ѧ��������һ�ο�ǰ������Ŀ���ԣ��Ѳ��Խ����Ϊ�ĸ��ȼ���A�������㣻B�������ã�C��������D���������������Խ�����������������������ͳ��ͼ�������ͳ��ͼ�е���Ϣ����������⣺ 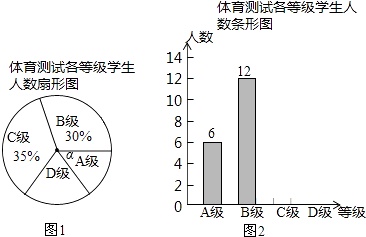
��1���뽫������������ͳ��ͼ����������
��2������õزμ��п���ѧ������4500�������ݲ������������Ʋ�����������ж��٣�
��3���ӱ�����ѧ������ѡһ��ѧ����������ѧ���ɼ���D���ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1���������� y=�� ![]() x2ƽ�ƺ����A��8��0����ԭ�㣬����ΪB���Գ�����x���ཻ�ڵ�C����ԭ�������ཻ�ڵ�D��
x2ƽ�ƺ����A��8��0����ԭ�㣬����ΪB���Գ�����x���ཻ�ڵ�C����ԭ�������ཻ�ڵ�D��
��1����ƽ�ƺ������ߵĽ���ʽ����D�����ꣻ
��2��ֱ��д����Ӱ���ֵ���� S��Ӱ��
��3����ͼ��2����ֱ��AB��y���ཻ�ڵ�P����MΪ�߶�OA��һ���㣨��M�����A��O�غ� ������PMNΪֱ�ǣ�MN��AP�ཻ�ڵ�N����OM=t����̽����tΪ��ֵʱ����MANΪ���������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺��ͼ�٣�����ı���ABCD����AB=AD��CB=CD����B=��D=90�㣬��ô���ǰ��������ı��ν������������Ρ���
��һ����ͼ����ʾ�ġ��������Ρ�ֽƬABCD���۵�����ͼ����ʾ��״����չ���õ�ͼ�ۣ�����CE��CFΪ�ۺۣ���BCE=��ECF=��FCD����B��Ϊ��B�Ķ�Ӧ�㣬��D��Ϊ��D�Ķ�Ӧ�㣬����EB�䣬FD���ཻ�ڵ�O��
��1����ƽ���ı��Ρ����Ρ����Ρ�����������ͼ���У�һ��Ϊ���������Ρ�����
��2����ͼ���еġ�BCD=120��ʱ����AEB��=
��3����ͼ���е��ı���AECFΪ����ʱ����Ӧͼ���еġ��������Ρ��С� ���������ı���ABCD����
��4����չ��������ͼ���еġ�BCD=90��ʱ������AB�䣬��̽���AB��E�Ķ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com