
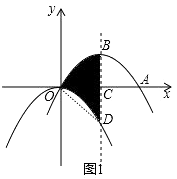
【题目】如图(1),抛物线 y=﹣ ![]() x2平移后过点A(8,0)和原点,顶点为B,对称轴与x轴相交于点C,与原抛物线相交于点D.
x2平移后过点A(8,0)和原点,顶点为B,对称轴与x轴相交于点C,与原抛物线相交于点D.
(1)求平移后抛物线的解析式及点D的坐标;
(2)直接写出阴影部分的面积 S阴影;
(3)如图(2),直线AB与y轴相交于点P,点M为线段OA上一动点(点M不与点A,O重合 ),∠PMN为直角,MN与AP相交于点N,设OM=t,试探究:t为何值时,△MAN为等腰三角形?
【答案】
(1)
解:平移后的抛物线解析式为y=﹣ ![]() x(x﹣8),
x(x﹣8),
即y=﹣ ![]() x2+
x2+ ![]() x
x
(2)
解:如图1,连接OB、OD,
y=﹣ ![]() (x﹣4)2+3,则B(4,3)
(x﹣4)2+3,则B(4,3)
平移后的抛物线的对称轴为直线x=4,
当x=4时,y=﹣ ![]() x2=﹣3,则D(4,﹣3),
x2=﹣3,则D(4,﹣3),
∴点B与点D关于x轴对称,
∴阴影部分的面积 S阴影=S△OBD= ![]() ×3×(4+4)=12
×3×(4+4)=12
(3)
解:设直线AB的解析式为y=kx+b,
把A(8,0),B(4,3)代入得 ![]() ,解得
,解得  ,
,
∴直线AB的解析式为y=﹣ ![]() x+6,
x+6,
作NQ⊥x轴于Q,如图2,P(0,6),AP=10,
∵∠PMN为直角,
∴∠PMO+∠QMN=90°,
而∠PMO+∠MOP=90°,
∴∠QMN=∠MOP,
∴△MPO∽△NMQ,
∴ ![]() =
= ![]() ,
,
当NM=NA时,MQ=AQ= ![]() (8﹣t),
(8﹣t),
∴OQ=8﹣ ![]() (8﹣t)=
(8﹣t)= ![]() t+4,
t+4,
当x= ![]() t+4时,y=﹣
t+4时,y=﹣ ![]() (
( ![]() t+4)+6=﹣
t+4)+6=﹣ ![]() t+3;
t+3;
∴ ![]() =
= ![]() ,解得t1=8(舍去),t2=
,解得t1=8(舍去),t2= ![]() ;
;
当AM=AN时,AN=AM=8﹣t,
∵NQ∥OP,
∴△ANQ∽△APO,
∴ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= ![]() ,
,
∴NQ= ![]() (8﹣t),AQ=
(8﹣t),AQ= ![]() (8﹣t),
(8﹣t),
∴MQ=8﹣t﹣ ![]() (8﹣t)=
(8﹣t)= ![]() ,
,
∴ ![]() =
= ![]() ,解得t1=8(舍去),t2=18(舍去;
,解得t1=8(舍去),t2=18(舍去;
当MA=MN时,
∵∠OAP<45°,
∴∠MNA=∠NAM<45°,
∴∠AMN>90°,显然不成立,
综上所述,当t为 ![]() 时,△MAN为等腰三角形
时,△MAN为等腰三角形

【解析】(1)利用交点式写出平移后的抛物线解析式;(2)如图1,连接OB、OD,先通过配方法可得到B(4,3),再确定D(4,﹣3),利用对称性可得到阴影部分的面积 S阴影=S△OBD , 然后根据三角形面积公式求解;(3)先利用待定系数法求出直线AB的解析式为y=﹣ ![]() x+6,作NQ⊥x轴于Q,如图2,易得P(0,6),AP=10,再证明△MPO∽△NMQ得到
x+6,作NQ⊥x轴于Q,如图2,易得P(0,6),AP=10,再证明△MPO∽△NMQ得到 ![]() =
= ![]() ,然后讨论:当NM=NA时,MQ=AQ=
,然后讨论:当NM=NA时,MQ=AQ= ![]() (8﹣t),则OQ=
(8﹣t),则OQ= ![]() t+4,接着利用一次函数图象上点的坐标表示出NQ=﹣
t+4,接着利用一次函数图象上点的坐标表示出NQ=﹣ ![]() t+3,则利用相似比得到
t+3,则利用相似比得到 ![]() =
= ![]() ,解方程求出满足条件的t的值;当AM=AN时,AN=AM=8﹣t,证明△ANQ∽△APO,利用相似比可得到NQ=
,解方程求出满足条件的t的值;当AM=AN时,AN=AM=8﹣t,证明△ANQ∽△APO,利用相似比可得到NQ= ![]() (8﹣t),AQ=
(8﹣t),AQ= ![]() (8﹣t),则MQ=8﹣t﹣
(8﹣t),则MQ=8﹣t﹣ ![]() (8﹣t)=
(8﹣t)= ![]() ,然后利用相似比得到
,然后利用相似比得到 ![]() =
= ![]() ,解方程确定满足条件的t的值;当MA=MN时,由于∠OAP<45°,则∠MNA=∠NAM<45°,原式可判断∠AMN>90°,显然不成立,所以当t为
,解方程确定满足条件的t的值;当MA=MN时,由于∠OAP<45°,则∠MNA=∠NAM<45°,原式可判断∠AMN>90°,显然不成立,所以当t为 ![]() 时,△MAN为等腰三角形.
时,△MAN为等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标中,点A的坐标为(1,﹣2),点B的坐标为(3,﹣1),二次函数y=﹣x2的图象为l1 . 
(1)平移抛物线l1 , 使平移后的抛物线经过点A,但不过点B.
①满足此条件的函数解析式有个.
②写出向下平移且经点A的解析式 .
(2)平移抛物线l1 , 使平移后的抛物线经过A,B两点,所得的抛物线l2 , 如图②,求抛物线l2的函数解析式及顶点C的坐标,并求△ABC的面积.
(3)在y轴上是否存在点P,使S△ABC=S△ABP?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA是⊙M的直径,点B在x轴上,连接AB交⊙M于点C. 
(1)若点A的坐标为(0,2),∠ABO=30°,求点B的坐标.
(2)若D为OB的中点,求证:直线CD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于F,且AF=BD,连接BF. 
(1)求证:D是BC的中点.
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学同时为校文化艺术节制作彩旗.已知甲每小时比乙多做5面彩旗,甲做60面彩旗与乙做50面彩旗所用时间相等,问:甲、乙每小时各做多少面彩旗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AB=6,AD⊥BC于点D.点P在边AB上运动,过点P作PE∥BC,与边AC交于点E,连结ED,以PE、ED为邻边作PEDF.设PEDF与△ABC重叠部分图形的面积为y,线段AP的长为x(0<x<6).
(1)求线段PE的长.(用含x的代数式表示)
(2)当四边形PEDF为菱形时,求x的值.
(3)求y与x之间的函数关系式.
(4)设点A关于直线PE的对称点为点A′,当线段A′B的垂直平分线与直线AD相交时,设其交点为Q,当点P与点Q位于直线BC同侧(不包括点Q在直线BC上)时,直接写出x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com