
【题目】如图,△ABC中,CD是边AB上的高,且![]() =
=![]()

(1)求证:△ACD∽△CBD
(2)求∠ACB的大小
【答案】
(1)
证明:∵CD是边AB上的高,
∴∠ADC=∠CDB=90°,
∵![]() =
=![]() .
.
∴△ACD∽△CBD
(2)
解:∵△ACD∽△CBD,
∴∠A=∠BCD,
在△ACD中,∠ADC=90°,
∴∠A+∠ACD=90°,
∴∠BCD+∠ACD=90°,
即∠ACB=90°.
【解析】(1)由两边对应成比例且夹角相等的两个三角形相似,即可证明△ACD∽△CBD;
(2)由(1)知△ACD∽△CBD,然后根据相似三角形的对应角相等可得:∠A=∠BCD,然后由∠A+∠ACD=90°,可得:∠BCD+∠ACD=90°,即∠ACB=90°.
【考点精析】根据题目的已知条件,利用相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】探究题
如图1,等边△ABC中,BC=4,点P从点B出发,沿BC方向运动到点C,点P关于直线AB、AC的对称点分别为点M、N,连接MN.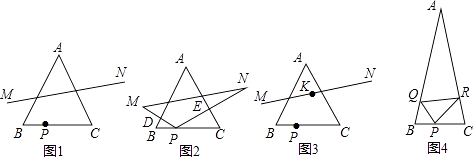
(1)【发现】
当点P与点B重合时,线段MN的长是 .
当AP的长最小时,线段MN的长是;
(2)【探究】
如图2,设PB=x,MN2=y,连接PM、PN,分别交AB,AC于点D,E.
用含x的代数式表示PM= , PN=;
(3)求y关于x的函数关系式,并写出y的取值范围;
(4)当点P在直线BC上的什么位置时,线段MN=3 ![]() (直接写出答案)
(直接写出答案)
(5)【拓展】
如图3,求线段MN的中点K经过的路线长.
(6)【应用】
如图4,在等腰△ABC中,∠BAC=30°,AB=AC,BC=2,点P、Q、R分别为边BC、AB、AC上(均不与端点重合)的动点,则△PQR周长的最小值是 .
(可能用到的数值:sin75°= ![]() ,cos75°=
,cos75°= ![]() ,tan75°=2+
,tan75°=2+ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),抛物线 y=﹣ ![]() x2平移后过点A(8,0)和原点,顶点为B,对称轴与x轴相交于点C,与原抛物线相交于点D.
x2平移后过点A(8,0)和原点,顶点为B,对称轴与x轴相交于点C,与原抛物线相交于点D.
(1)求平移后抛物线的解析式及点D的坐标;
(2)直接写出阴影部分的面积 S阴影;
(3)如图(2),直线AB与y轴相交于点P,点M为线段OA上一动点(点M不与点A,O重合 ),∠PMN为直角,MN与AP相交于点N,设OM=t,试探究:t为何值时,△MAN为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店打出促销广告:最潮新款服装30件,每件售价300元.若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低3元.已知该服装成本是每件200元,设顾客一次性购买服装x件时,该网店从中获利y元.
(1)求y与x的函数关系式,并写出自变量x的取值范围。
(2)顾客一次性购买多少件时,该网店从中获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)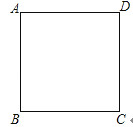
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:如图①,如果四边形ABCD满足AB=AD,CB=CD,∠B=∠D=90°,那么我们把这样的四边形叫做“完美筝形”.
将一张如图①所示的“完美筝形”纸片ABCD先折叠成如图②所示形状,再展开得到图③,其中CE,CF为折痕,∠BCE=∠ECF=∠FCD,点B′为点B的对应点,点D′为点D的对应点,连接EB′,FD′相交于点O.
(1)在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是
(2)当图③中的∠BCD=120°时,∠AEB′=
(3)当图②中的四边形AECF为菱形时,对应图③中的“完美筝形”有 个(包含四边形ABCD).
(4)拓展提升:当图③中的∠BCD=90°时,连接AB′,请探求∠AB′E的度数,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分的进水量和出水量有两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.
(1)当4≤x≤12时,求y关于x的函数解析式;
(2)直接写出每分进水,出水各多少升.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣x+3与x轴、y轴分别交于A,B两点,抛物线y=﹣x2+bx+c经过A,B两点,点P在线段OA上,从点O出发,向点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以![]() 个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
(1)求抛物线的解析式;
(2)问:当t为何值时,△APQ为直角三角形;
(3)过点P作PE∥y轴,交AB于点E,过点Q作QF∥y轴,交抛物线于点F,连接EF,当EF∥PQ时,求点F的坐标.
(4)设抛物线顶点为M,连接BP,BM,MQ,问:是否存在t的值,使以B,Q,M为顶点的三角形与以O,B,P为顶点的三角形相似?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com