
����Ŀ��̽����
��ͼ1���ȱߡ�ABC�У�BC=4����P�ӵ�B��������BC�����˶�����C����P����ֱ��AB��AC�ĶԳƵ�ֱ�Ϊ��M��N������MN��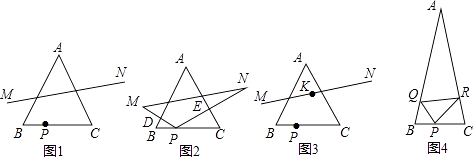
��1�������֡�
����P���B�غ�ʱ���߶�MN�ij��� ��
��AP�ij���Сʱ���߶�MN�ij�����
��2����̽����
��ͼ2����PB=x��MN2=y������PM��PN���ֱ�AB��AC�ڵ�D��E��
�ú�x�Ĵ���ʽ��ʾPM= �� PN=��
��3����y����x�ĺ�����ϵʽ����д��y��ȡֵ��Χ��
��4������P��ֱ��BC�ϵ�ʲôλ��ʱ���߶�MN=3 ![]() ��ֱ��д���𰸣�
��ֱ��д���𰸣�
��5������չ��
��ͼ3�����߶�MN���е�K������·�߳���
��6����Ӧ�á�
��ͼ4���ڵ�����ABC�У���BAC=30�㣬AB=AC��BC=2����P��Q��R�ֱ�Ϊ��BC��AB��AC�ϣ�������˵��غϣ��Ķ��㣬���PQR�ܳ�����Сֵ�� ��
�������õ�����ֵ��sin75��= ![]() ��cos75��=
��cos75��= ![]() ��tan75��=2+
��tan75��=2+ ![]() ��
��
���𰸡�
��1��4 ![]() ��6
��6
��2��![]()
x��![]()
��4��x��
��3��
�⣺

��ͼ2���ֱ����M��N��ֱ��BC�Ĵ���MF��NG������ֱ���F��G������M��MH��NG����ΪH��
����Rt��PMF�У���MPF=30�㣬PM= ![]() x��
x��
��MF= ![]() x��PF=
x��PF= ![]() x��
x��
ͬ������Rt��PNG�У���NPG=30�㣬PN= ![]() ��4��x����
��4��x����
��NG= ![]() ��4��x����PG=
��4��x����PG= ![]() ��4��x����
��4��x����
���ı���MFGH�Ǿ��Σ�����
NH=NG��HG=NG��MF= ![]() ��4��x����
��4��x���� ![]() x=
x= ![]() ��2��x����
��2��x����
MH=FG=PF+PG= ![]() x+
x+ ![]() ��4��x��=6��
��4��x��=6��
����Rt��MNH�У��ɹ��ɶ����ã�
MN2=NH2+MH2=3��x��2��2+36��
��y=3��x��2��2+36��
��0��x��4���ҵ�x=2ʱ��y��Сֵ=36����x=0��4ʱ��y���ֵ=48��
��36��y��48
��4��
�⣺��MN=3 ![]() ��MN2=63��
��MN2=63��
�൱y=63ʱ����3��x��2��2+36=63��
��x=5��1��
�൱��P��B���Ҳ����Ϊ5�������ڵ�P��B��������Ϊ1��λ�ô��������߶�MN=3 ![]()
��5��
�⣺��ͼ3���ֱ����M��N��ֱ��BC�Ĵ���MF��NG������ֱ���F��G������MG����MN���е�K����KT��BC�ڵ�T����MG�ڵ�S��
��MF��KT��NG���ҵ�KΪMN���е㣬
��KS�ǡ�MNG����λ�ߣ�
ST�ǡ�GMF����λ�ߣ�

��6��2+ ![]()
���������⣺�����֡���AP�ij���Сʱ��AP��BC������PΪBC���е�ʱ��
��ʱE��F�ֱ�ΪAB��AC���е㣬
��PE= ![]() AC��PF=
AC��PF= ![]() AB��EF=
AB��EF= ![]() BC��
BC��
��MN=ME+EF+FN=PE+EF+PF=6��
����P�͵�B�غ�ʱ��
��ʱG��H��ΪAB��AC�����е㣬
��CG=2 ![]() BH=2
BH=2 ![]() ��
��
BN=4 ![]() ��
��
���Դ��ǣ�4 ![]() ��6��
��6��
��̽����PM=2PD=2�� ![]() PB=
PB= ![]() x��PN=2PE=2��
x��PN=2PE=2�� ![]() PC=2��
PC=2�� ![]() ��4��x��=
��4��x��= ![]() ��4��x����
��4��x����
���Դ��ǣ� ![]() x��
x�� ![]() ��4��x����
��4��x����
����չ��
�ɡ�̽�����еĹ��̿�֪������PB=x������PC=4��x��MF= ![]() x��NG=
x��NG= ![]() ��4��x����
��4��x����
����������λ�����ʿɵã�ST= ![]() MF=
MF= ![]() x��KS=
x��KS= ![]() NG=
NG= ![]() ��4��x����
��4��x����
��KT=ST+KS= ![]() x+
x+ ![]() ��4��x��=
��4��x��= ![]() ��
��
��ˣ��ڵ�P�˶������У�MN���е� K��BC�߾���ʼ�յ��ڶ�ֵ ![]() ����Ϊ
����Ϊ
�ȱߡ�ABC�ߵ�һ�룬����MN���е�K������·��ǡΪ�ȱߡ�ABC����λ�ߣ���·�߳�Ϊ2��
��Ӧ�á���BC���е�P��AB��AC�ĶԳƵ�M��N������MN��AB��Q����AC��R��
���ʱ��PQR�ܳ���С��
�ߡ�BAC=30�㣬
���B=��C=75�㣬��MPN=150�㣬
���M=��N=15�㣬
���MQB=��PQB=��B=75�㣬
��MN��BC��PQ=PB=1��
ͬ��PR=PC=1��
��AP��BC��
��AP��MN��
�ߡ�PQR=180�㩁75�㩁75��=30�㣬
��QR=2�� ![]() PQ=
PQ= ![]() ��
��
���PQR�ܳ�����Сֵ��2+ ![]() ��
��
���Դ��ǣ�2+ ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����������ε������ߵı߳�֮��3��2����������������εǵ�����ֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ����һRt��AOB��OΪ����ԭ�㣬OA=1��tan��BAO=3��������������ԭ��O��ʱ����ת90�㣬�õ���DOC��������l��y=��x2+bx+c����A��B���㣮
��1����������l�Ľ���ʽ������G�����꣮
��2������֤��������l������C��
�ڷֱ�����CG��DG�����GCD�������
��3���ڵڶ������ڣ��������ϴ������ڵ�G��һ��P��ʹ��PCD���CDG�������ȣ���ֱ��д����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���糿�ܲ��������Լ��ҳ�����������2km����С��ң�����������1.5km����С��ң�Ȼ������������4.5km����ѧУ����������ܻص��Լ��ң�
��1����С����Ϊԭ�㣬����Ϊ��������1����λ���ȱ�ʾ1km����ͼ�е������ϣ��ֱ��õ�A��ʾ��С��ң��õ�B��ʾ��С��ң��õ�C��ʾ��ѧУ��λ�ã�![]()
��2����С�����ѧУ֮��ľ��룻
��3�����С���ܲ����ٶ���250m/min����ôС���ܲ�һ�����˶ʱ�䣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����y=2x��y=��x��ͼ��ֱ�Ϊֱ��l1 �� l2 �� ���㣨1��0����x��Ĵ��߽�l1�ڵ�A1 �� ����A1��y��Ĵ��߽�l2�ڵ�A2 �� ����A2��x��Ĵ��߽�l1�ڵ�A3 �� ����A3��y��Ĵ��߽�l2�ڵ�A4 �� �����ν�����ȥ�����A2017������Ϊ �� A2n+1������Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���ƽ��ֱ�������У���A������Ϊ��1����2������B������Ϊ��3����1�������κ���y=��x2��ͼ��Ϊl1 �� 
��1��ƽ��������l1 �� ʹƽ�ƺ�������߾�����A����������B��
������������ĺ�������ʽ������
��д������ƽ���Ҿ���A�Ľ���ʽ ��
��2��ƽ��������l1 �� ʹƽ�ƺ�������߾���A��B���㣬���õ�������l2 �� ��ͼ�ڣ���������l2�ĺ�������ʽ������C�����꣬�����ABC�������
��3����y�����Ƿ���ڵ�P��ʹS��ABC=S��ABP�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OA�ǡ�M��ֱ������B��x���ϣ�����AB����M�ڵ�C�� 
��1������A������Ϊ��0��2������ABO=30�㣬���B�����꣮
��2����DΪOB���е㣬��֤��ֱ��CD�ǡ�O�����ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�CD�DZ�AB�ϵĸߣ���![]() =
=![]()

��1����֤����ACD�ס�CBD
��2�����ACB�Ĵ�С
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com