
【题目】从﹣4、3、5这三个数中,随机抽取一个数,记为a,那么,使关于x的方程x2+4x+a=0有解,且使关于x的一次函数y=2x+a的图象与x轴、y轴围成的三角形面积恰好为4的概率_____.
科目:初中数学 来源: 题型:
【题目】已知:如图1,点A (1, 0),B(0,2),将点B沿x轴正方向平移3个单位长度得到对应点B′,点B′ 恰在反比例函数y=![]() (x>0)的图象上.
(x>0)的图象上.
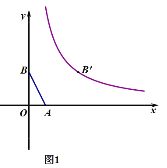
(1)求k的值;
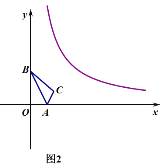
(2)如图2,将△AOB (点O为坐标原点)沿AB翻折得到△ACB,求点C的坐标;
(3)是否存在这样的点P,以P为位似中心,将△AOB放大为原来的两倍后得到△DEF (即△DEF∽△AOB,且相似比为2),使得点D、F恰好在反比例函数y=![]() (x>0) 的图象上?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
(x>0) 的图象上?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学所在年级的500名学生参加志愿者活动,现有以下5个志愿服务项目:A,纪念馆志讲解员.B.书香社区图书整理C.学编中国结及义卖.D,家风讲解员E.校内志愿服务,要求:每位学生都从中选择一个项目参加,为了了解同学们选择这个5个项目的情况,该同学随机对年级中的40名同学选择的志愿服务项目进行了调查,过程如下:
收集数据:设计调查问卷,收集到如下数据(志愿服务项目的编号,用字母代号表示)
B,E,B,A,E,C,C,C,B,B,
A,C,E,D,B,A,B,E,C,A,
D,D,B,B,C,C,A,E,B
C,B,D,C,A,C,C,A,C,E,
(1)整理、描述诗句:划记、整理、描述样本数据,绘制统计图如下,请补全统计表和统计图

选择各志愿服务项目的人数统计表
志愿服务项目 | 划记 | 人数 |
A.纪念馆志愿讲解员 | 正 | 8 |
B.书香社区图书整理 | ||
C.学编中国结及义卖 | 正正 | 12 |
D.家风讲解员 | ||
E.校内志愿服务 | 正 一 | 6 |
合计 | 40 | 40 |
分析数据、推断结论
(2)抽样的40个样本数据(志愿服务项目的编号)的众数是 (填A﹣E的字母代号)
(3)请你任选A﹣E中的两个志愿服务项目,根据该同学的样本数据估计全年级大约有多少名同学选择这两个志愿服务项目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 和
和![]()
(1)如何将抛物线![]() 平移得到抛物线
平移得到抛物线![]() ?
?
(2)如图1,抛物线![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() ,交抛物线
,交抛物线![]() 于另一点
于另一点![]() .请你在线段
.请你在线段![]() 上取点
上取点![]() ,过点
,过点![]() 作直线
作直线![]() 轴交抛物线
轴交抛物线![]() 于点
于点![]() ,连接
,连接![]()

①若![]() ,求点
,求点![]() 的横坐标
的横坐标
②若![]() ,直接写出点
,直接写出点![]() 的横坐标
的横坐标
(3)如图2,![]() 的顶点
的顶点![]() 、
、![]() 在抛物线
在抛物线![]() 上,点
上,点![]() 在点
在点![]() 右边,两条直线
右边,两条直线![]() 、
、![]() 与抛物线
与抛物线![]() 均有唯一公共点,
均有唯一公共点,![]() 、
、![]() 均与
均与![]() 轴不平行.若
轴不平行.若![]() 的面积为2,设
的面积为2,设![]() 、
、![]() 两点的横坐标分别为
两点的横坐标分别为![]() 、
、![]() ,求
,求![]() 与
与![]() 的数量关系
的数量关系

查看答案和解析>>
科目:初中数学 来源: 题型:
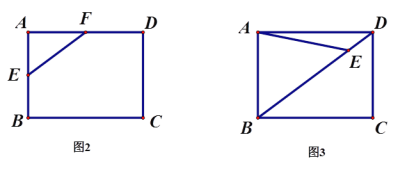
【题目】按要求作图,不要求写作法,但要保留作图痕迹.
(1)如图1,矩形ABCD的顶点A、D在圆上, B、C两点在圆内,已知圆心O,请仅用无刻度的直尺作图,请作出直线l⊥AD;
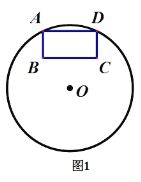
(2)请仅用无刻度的直尺在下列图2和图3中按要求作图.(补上所作图形顶点字母)
①图2是矩形ABCD,E,F分别是AB和AD的中点,以EF为边作一个菱形;
②图3是矩形ABCD,E是对角线BD上任意一点(BE>DE),以AE为边作一个平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园读诗词诵经典比赛”结束后,评委刘老师将此次所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图,部分信息如下图:
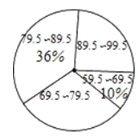
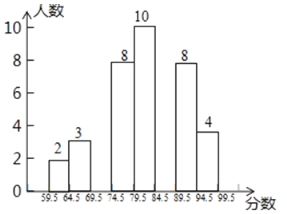
扇形统计图 频数直方图
(1)参加本次比赛的选手共有________人,参赛选手比赛成绩的中位数在__________分数段;补全频数直方图.
(2)若此次比赛的前五名成绩中有![]() 名男生和
名男生和![]() 名女生,如果从他们中任选
名女生,如果从他们中任选![]() 人作为获奖代表发言,请利用表格或画树状图求恰好选中
人作为获奖代表发言,请利用表格或画树状图求恰好选中![]() 男
男![]() 女的概率.
女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若用“*”表示一种运算规则,我们规定:a*b=ab﹣a+b,如:3*2=3×2﹣3+2=5.以下说法中错误的是( )
A. 不等式(﹣2)*(3﹣x)<2的解集是x<3
B. 函数y=(x+2)*x的图象与x轴有两个交点
C. 在实数范围内,无论a取何值,代数式a*(a+1)的值总为正数
D. 方程(x﹣2)*3=5的解是x=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情景:一节数学课后,老师布置了一道练习题:
如图1,已知Rt△ABC中,AC=BC,∠ABC=90°,CD⊥AB于点D,点E,F分别在AD和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF
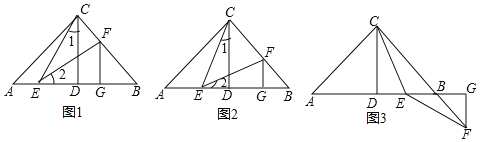
(1)阅读理解,完成解答:本题证明的思路可以用下列框图表示:
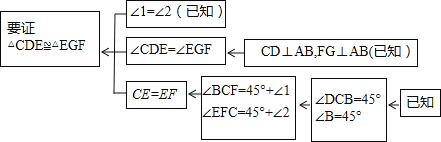
根据上述思路,请你完整地写出这道练习题的证明过程;
(2)特殊位置,证明结论:如图2,若CE平分∠ACD,其余条件不变,判断AE和BF的数量关系,并说明理由;
(3)知识迁移.探究发现:如图3,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上,且EC=EF,请直接写出BF与AE的数量关系.(不必写解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得_______________;
(Ⅱ)解不等式②,得_______________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(Ⅳ)原不等式组的解集为______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com