
【题目】某经销商从市场得知如下信息:
A 品牌手表 | B 品牌手表 | |
进价(元/块) | 700 | 100 |
售价(元/块) | 900 | 160 |
他计划用 40000 元资金一次性购进这两种品牌手表共 100 块,设该经销商购进 A 品牌手表 x 块,这两种品牌手表全部销售完后获得利润为 y 元.
(1)试写出 y 与 x 之间的函数关系式;
(2)若要求全部销售完后获得的利润不少于 12650 元,该经销商有哪几种进货方案;
(3)选择哪种进货方案,该经销商可获利最大;最大利润是多少元.
【答案】(1)y=140x+6000(0<x≤50);(2)经销商有以下三种进货方案:①A型48,B型52,②A型49,B型51,③A型50,B型50;(3)选择方案③进货时,经销商可获利最大,最大利润是13000元.
【解析】
(1)根据利润y=(A售价-A进价)×A手表的数量+(B售价-B进价)×B手表的数量,根据总资金不超过4万元得出x的取值范围,列式整理即可;
(2)全部销售后利润不少于12650元.得到一元一次不等式组,求出满足题意的x的正整数值即可;
(3)利用y与x的函数关系式的增减性来选择哪种方案获利最大,并求此时的最大利润即可.
解:(1)y=(900-700)x+(160-100)×(100-x)
=140x+6000,
其中700x+100(100-x)≤40000,
得x≤50,
即y=140x+6000(0<x≤50);
(2)令y≥12650,
则140x+6000≥12650,
∴x≥47.5,
又∵x≤50,x为整数
∴48≤x≤50
∴经销商有以下三种进货方案:

(3)∵y=140x+6000,140>0,
∴y随x的增大而增大,
∴x=50时,y取得最大值,
又∵140×50+6000=13000,
∴选择方案③进货时,经销商可获利最大,最大利润是13000元.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】如图所示,运载火箭从地面L处垂直向上发射,当火箭到达A点时,从位于地面R处的雷达测得AR的距离是40km,仰角是30°,n秒后,火箭到达B点,此时仰角是45°,则火箭在这n秒中上升的高度是_____km.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,两线相交于F点.
(1)若∠BAC=60°,∠C=70°,求∠AFB的大小;
(2)若D是BC的中点,∠ABE=30°,求证:△ABC是等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣x+3与抛物线![]() 交于A、B两点,点A在x轴上,点B的横坐标为
交于A、B两点,点A在x轴上,点B的横坐标为![]() .动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
.动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
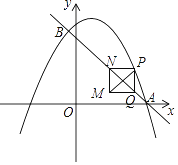
(1)求b、c的值.
(2)当点N落在直线AB上时,直接写出m的取值范围.
(3)当点P在A、B两点之间的抛物线上运动时,设正方形PQMN的周长为C,求C与m之间的函数关系式,并写出C随m增大而增大时m的取值范围.
(4)当△PQM与坐标轴有2个公共点时,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图1、图2、图3分别表示甲、乙、丙三人由甲A地到B地的路线图(箭头表示行进的方向).其中E为AB的中点,AH>HB,判断三人行进路线长度的大小关系为

A.甲<乙<丙 B.乙<丙<甲 C.丙<乙<甲 D.甲=乙=丙
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知BD是△ABC的角平分线,点E在边AB上,BC=BE,过点E作EF∥AC,交BD于点F,连接CF.
(1)如图1,求证:四边形CDEF是菱形;
(2)如图2,当四边形CDEF是正方形,且AC=BC时,在不添加辅助线的情况下,请直接写出图中度数等于30°的角.
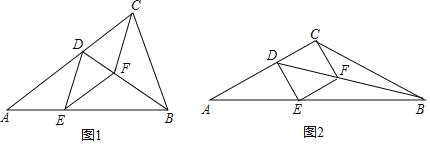
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() (其中
(其中![]() 为常数,
为常数,![]() ),
),![]() 取不同数值时,可得不同直线,请研究这些直线的共同特征.
取不同数值时,可得不同直线,请研究这些直线的共同特征.
实践操作
(1)当![]() 时,直线
时,直线![]() 的解析式为________,请在图1中画出图象.
的解析式为________,请在图1中画出图象.
当![]() 时,直线
时,直线![]() 的解析式为________,请在图2中画出图象
的解析式为________,请在图2中画出图象
(2)探索发现:
直线![]() 必经过点(_______,_______).
必经过点(_______,_______).
(3)类比迁移:
矩形![]() 如图2所示,若直线
如图2所示,若直线![]() 分矩形
分矩形![]() 的面积为相等的两部分,请在图中直接画出这条直线.
的面积为相等的两部分,请在图中直接画出这条直线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中装有3个带号码的球,球号分别为2,3,4,这些球除号码不同外其它均相同。甲、乙、两同学玩摸球游戏,游戏规则如下:
先由甲同学从中随机摸出一球,记下球号,并放回搅匀,再由乙同学从中随机摸出一球,记下球号。将甲同学摸出的球号作为一个两位数的十位上的数,乙同学的作为个位上的数。若该两位数能被4整除,则甲胜,否则乙胜.
问:这个游戏公平吗?请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com