
【题目】如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
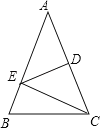
(1)求∠ECD的度数;
(2)若CE=5,求BC长.
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线l1:y=x+3与x轴交于点A,与y轴交于点B,与直线l2:y=﹣![]() x交于点P.直线l3:y=﹣
x交于点P.直线l3:y=﹣![]() x+4与x轴交于点C,与y轴交于点D,与直线l1交于点Q,与直线l2交于点R.
x+4与x轴交于点C,与y轴交于点D,与直线l1交于点Q,与直线l2交于点R.
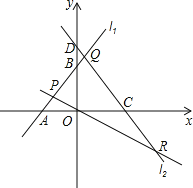
(1)点A的坐标是 ,点B的坐标是 ,点P的坐标是 ;
(2)将△POB沿y轴折叠后,点P的对应点为P′,试判断点P′是否在直线l3上,并说明理由;
(3)求△PQR的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有理数a大于有理数b,则( )
A. a的绝对值大于b的绝对值
B. a的绝对值小于b的绝对值
C. a的相反数大于b的相反数
D. a的相反数小于b的相反数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.
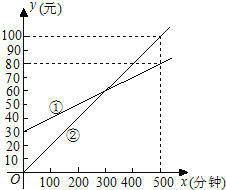
(1)有月租费的收费方式是 (填①或②),月租费是 元;
(2)分别求出①、②两种收费方式中y与自变量x之间的函数关系式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C是半圆O上的一点,BD与过点C的直线互相垂直,垂足为点D,BD与半圆O交于点E,且BC平分∠DBA.
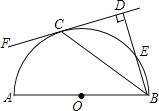
(1)求证:CD是半圆O的切线.
(2)若DC=8,BE=4,求圆的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),
其中正确结论的个数是( )
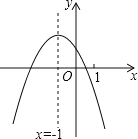
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上有A、B两点,A在B的左侧,已知点B对应的数为2,点A对应的数为a.
(1)若a=﹣3,则线段AB的长为 (直接写出结果);
(2)若点C在线段AB之间,且AC﹣BC=2,求点C表示的数(用含a的式子表示);
(3)在(2)的条件下,点D是数轴上A点左侧一点,当AC=2AD,BD=4BC,求a的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com