
【题目】如图,AB是半圆O的直径,C是半圆O上的一点,BD与过点C的直线互相垂直,垂足为点D,BD与半圆O交于点E,且BC平分∠DBA.
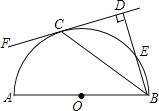
(1)求证:CD是半圆O的切线.
(2)若DC=8,BE=4,求圆的直径.
【答案】(1)见解析;(2)4![]() .
.
【解析】
试题分析:(1)首先连接OC,由OB=OC,BC平分∠DBA,易证得OC∥BD,又由BD⊥CD,即可证得结论;
(2)首先根据切割线定理求得BD,然后根据勾股定理求得BC,连接AC,通过证得△ABC∽△CBD,然后由相似三角形的对应边成比例,求得AB.
(1)证明:连接OC,
∵OB=OC,
∴∠1=∠2,
∵BC平分∠DBA,
∴∠2=∠3,
∴∠1=∠3,
∴OC∥BD,
∵BD⊥CD,
∴OC⊥CD,
∵C是半圆O上的一点,
∴CD与半圆O相切;
(2)连接AC,
∵CD是切线,
∴CD2=DEBD,
∵DC=8,BE=4,
设BD=x,则82=x(x﹣4),
解得x=2+2![]() ,
,
∴BD=2![]() ,
,
∵∠BDC=90°,
∴BC2=CD2+BD2=64+(2+2![]() )2,
)2,
∵AB是直径,
∴∠ACB=90°=∠BDC,
∵∠BDC=∠ABC,
∴△CDB∽△ACB,
∴![]() ,
,
∴AB=![]() =4
=4![]() .
.


科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.方差越大,说明数据就越稳定
B.“预计本题的正确率是95%”表示100位考生中一定有95人做对
C.两边及其一边的对角对应相等的两个三角形一定全等
D.圆内接四边形对角互补
查看答案和解析>>
科目:初中数学 来源: 题型:
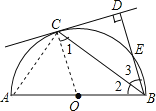
【题目】如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.
下面是一个案例,请补充完整.
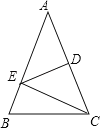
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.
(1)思路梳理
∵AB=AD
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合
∵∠ADC=∠B=90°
∴∠FDG=180°,点F、D、G共线根据SAS,易证△AFG≌ ,从而可得EF=BE+DF.
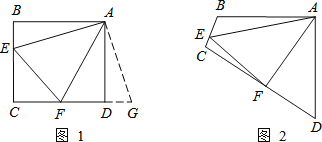
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在边BC、CD上,∠EAF=45°.若∠B、∠D都不是直角,则当∠B与∠D满足等量关系 时,仍有EF=BE+DF.
请写出推理过程:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽的家和学校在一条笔直的马路旁,某天小丽沿着这条马路上学,先从家步行到公交站台甲,再乘车到公交站台乙下车,最后步行到学校(在整个过程中小丽步行的速度不变),图中折线ABCDE表示小丽和学校之间的距离y(米)与她离家时间x(分钟)之间的函数关系.
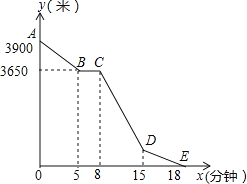
(1)求小丽步行的速度及学校与公交站台乙之间的距离;
(2)当8≤x≤15时,求y与x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=x+3分别交x轴、y轴于A,C两点,抛物线y=ax2+bx+c(a≠0),经过A,C两点,与x轴交于点B(1,0).
(1)求抛物线的解析式;
(2)点D为直线AC上一点,点E为抛物线上一点,且D,E两点的横坐标都为2,点F为x轴上的点,若四边形ADEF是平行四边形,请直接写出点F的坐标;
(3)若点P是线段AC上的一个动点,过点P作x轴的垂线,交抛物线于点Q,连接AQ,CQ,求△ACQ的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com