
【题目】通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.
下面是一个案例,请补充完整.
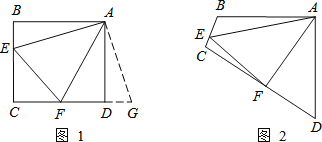
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.
(1)思路梳理
∵AB=AD
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合
∵∠ADC=∠B=90°
∴∠FDG=180°,点F、D、G共线根据SAS,易证△AFG≌ ,从而可得EF=BE+DF.
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在边BC、CD上,∠EAF=45°.若∠B、∠D都不是直角,则当∠B与∠D满足等量关系 时,仍有EF=BE+DF.
请写出推理过程:
【答案】(1)△AFE;(2)∠B+∠D=180°.
【解析】
试题分析:(1)把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,证出△AFG≌△AFE,根据全等三角形的性质得出EF=FG,即可得出答案;
(2)把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,证出△AFE≌△AFG,根据全等三角形的性质得出EF=FG,即可得出答案;
解:(1)理由是:如图1,
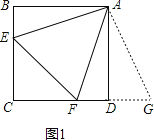
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,如图1,
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线,
则∠DAG=∠BAE,AE=AG,
∠FAG=∠FAD+∠GAD=∠FAD+∠BAE=90°﹣45°=45°=∠EAF,
即∠EAF=∠FAG,
在△EAF和△GAF中,
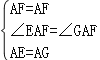 ,
,
∴△AFG≌△AFE(SAS),
∴EF=FG=BE+DF;
故答案为:△AFE;
(2)∠B+∠D=180°时,EF=BE+DF;
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,如图2,
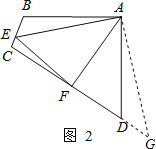
∴∠BAE=∠DAG,
∵∠BAD=90°,∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠EAF=∠FAG,
∵∠ADC+∠B=180°,
∴∠FDG=180°,点F、D、G共线,
在△AFE和△AFG中,
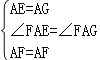 ,
,
∴△AFE≌△AFG(SAS),
∴EF=FG,
即:EF=BE+DF,
故答案为:∠B+∠D=180°.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.
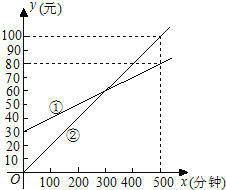
(1)有月租费的收费方式是 (填①或②),月租费是 元;
(2)分别求出①、②两种收费方式中y与自变量x之间的函数关系式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
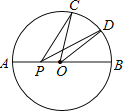
【题目】如图,已知⊙O的半径为2,C、D是直径AB同侧圆周上的两点,弧AC的度数是100°,D为弧BC的中点,动点P在直径AB上,则PC+PD的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C是半圆O上的一点,BD与过点C的直线互相垂直,垂足为点D,BD与半圆O交于点E,且BC平分∠DBA.
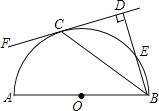
(1)求证:CD是半圆O的切线.
(2)若DC=8,BE=4,求圆的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个命题:①对顶角相等;②内错角相等;③平行于同一条直线的两条直线互相平行;④如果一个角的两边分别平行于另一个角的两边,那么这两个角相等。其中真命题的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列命题:①相等的角是对顶角;②互补的角一定是邻补角;③互补的两个角一定是一个锐角,另一个为钝角;④平行于同一条直线的两直线平行;⑤邻补角的平分线互相垂直.其中,真命题的个数为( )个
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com