
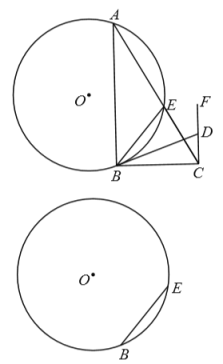
【题目】如图,![]() 是
是![]() 上的两个定点,
上的两个定点,![]() 为优弧
为优弧![]() 上的动点,过点
上的动点,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
(1)求证:![]() 与
与![]() 相切;
相切;
(2)已知:![]()
①若![]() ,求
,求![]() 的长;
的长;
②当![]() 两点间的距离最短时,判断
两点间的距离最短时,判断![]() 四点所组成的四边形的形状,并说明理由.
四点所组成的四边形的形状,并说明理由.
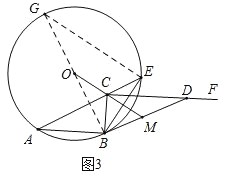
【答案】(1)详见解析;(2)①![]() ;②四边形
;②四边形![]() 是平行四边形,理由详见解析
是平行四边形,理由详见解析
【解析】
(1)如图1,作直径BG,连接GE,证∠EBD=∠G,则∠EBD+∠GBE=90°,即可推出结论;
(2)①如图2,连接AG,证△BCD∽△BAG,推出![]() ,在Rt△BGE中,求出BG的长,可进一步求出BD的长;
,在Rt△BGE中,求出BG的长,可进一步求出BD的长;
②由①推出![]() ,因为B,E为定点,BE为定值,所以BD为定值,D为定点,因为∠BCD=90°,所以点C在以BD为直径的⊙M上运动,当点C在线段OM上时,OC最小,证
,因为B,E为定点,BE为定值,所以BD为定值,D为定点,因为∠BCD=90°,所以点C在以BD为直径的⊙M上运动,当点C在线段OM上时,OC最小,证![]() ,∠OMB=60°,依次推出AB∥CD,AC∥BD即可.
,∠OMB=60°,依次推出AB∥CD,AC∥BD即可.
(1)如图1,作直径BG,连接GE,

则∠GEB=90°,
∴∠G+∠GBE=90°,
∵∠A=∠EBD,∠A=∠G,
∴∠EBD=∠G,
∴∠EBD+∠GBE=90°,
∴∠GBD=90°,
∴BD⊥OB,
∴BD与⊙O相切;
(2)①如图2,连接AG,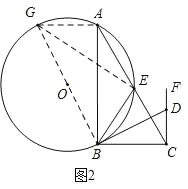
∵BC⊥AB,
∴∠ABC=90°,
由(1)知∠GBD=90°,
∴∠GBD=∠ABC,
∴∠GBA=∠CBD,
又∵∠GAB=∠DCB=90°,
∴△BCD∽△BAG,
∴![]()
又![]() 中,
中,![]() ,
,![]()
∴![]()
∴![]()
②四边形![]() 是平行四边形.理由如下:
是平行四边形.理由如下:
由①知![]() ,
,![]()
∴![]()
∵![]() 为定点,
为定点,![]() 为定值
为定值
∴![]() 为定值,
为定值,![]() 为定点
为定点
![]()
∴点![]() 在
在![]() 为直径的
为直径的![]() 上运动,
上运动,
∴当点![]() 在线段
在线段![]() 上时,
上时,![]() 最小
最小
此时在![]() 中,
中,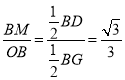
∴![]()
∴![]()
∴![]()
![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴四边形![]() 为平行四边形.
为平行四边形.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天府新区某校数学活动小组在一次活动中,对一个数学问题作如下探究:
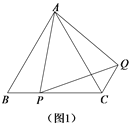
(1)问题发现:如图1,在等边△ABC中,点P是边BC上任意一点,连接AP,以AP为边作等边△APQ,连接CQ.求证:BP CQ;
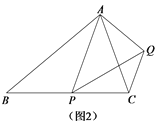
(2)变式探究:如图2,在等腰△ABC中,ABBC,点P是边BC上任意一点,以AP为腰作等腰△APQ,使AP PQ,APQ ABC,连接CQ.判断∠ABC和∠ACQ的数量关系,并说明理由;
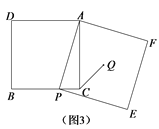
(3)解决问题:如图3,在正方形ADBC中,点P是边BC上一点,以AP为边作正方形 APEF,Q是正方形APEF的中心,连接CQ.若正方形APEF的边长为6,![]() ,求正方形ADBC的边长.
,求正方形ADBC的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.

(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
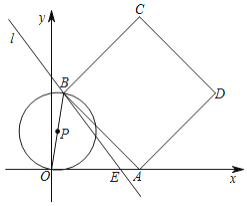
【题目】如图,已知直线![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 为
为![]() 轴上的一个动点(点
轴上的一个动点(点![]() 不与点
不与点![]() 重合),在直线
重合),在直线![]() 上取一点
上取一点![]() (点
(点![]() 在
在![]() 轴上方),使
轴上方),使![]() ,连结
,连结![]() ,以
,以![]() 为边在
为边在![]() 的右侧作正方形
的右侧作正方形![]() ,连结
,连结![]() ,以
,以![]() 为直径作
为直径作![]() .
.
(1)当点![]() 在点
在点![]() 左侧时,若点
左侧时,若点![]() 落在
落在![]() 轴上,则
轴上,则![]() 的长为______,点
的长为______,点![]() 的坐标为_______;
的坐标为_______;
(2)若![]() 与正方形
与正方形![]() 的边相切于点
的边相切于点![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)![]() 与直线
与直线![]() 的交点为
的交点为![]() ,连结
,连结![]() ,当
,当![]() 平分
平分![]() 时,
时,![]() 的长为______.(直接写出答案)
的长为______.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数![]() 的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数
的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数![]() 和y=x的图象于点C,D.
和y=x的图象于点C,D.
(1)求点A的坐标;
(2)若OB=CD,求a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程(请选择合适的方法)
(1)x2+4x=0;
(2)x2+![]() x﹣
x﹣![]() =0
=0
(3)3x(x﹣1)=4(x﹣1);
(4)x2﹣4x+4=(3﹣2x)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商计划购进甲、乙两种水果进行销售,经了解,甲种水果的进价比乙种水果的进价每千克少4元,且用800元购进甲种水果的数量与用1000元购进乙种水果的数量相同.
(1)求甲、乙两种水果的单价分别是多少元?
(2)该水果商根据该水果店平常的销售情况确定,购进两种水果共200千克,其中甲种水果的数量不超过乙种水果数量的3倍,且购买资金不超过3420元,购回后,水果商决定甲种水果的销售价定为每千克20元,乙种水果的销售价定为每千克25元,则水果商应如何进货,才能获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
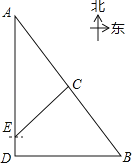
【题目】某校组织学生到恩格贝![]() 和康镇
和康镇![]() 进行研学活动,澄澄老师在网上查得,
进行研学活动,澄澄老师在网上查得,![]() 和
和![]() 分别位于学校
分别位于学校![]() 的正北和正东方向,
的正北和正东方向,![]() 位于
位于![]() 南偏东37°方向,校车从
南偏东37°方向,校车从![]() 出发,沿正北方向前往
出发,沿正北方向前往![]() 地,行驶到15千米的
地,行驶到15千米的![]() 处时,导航显示,在
处时,导航显示,在![]() 处北偏东45°方向有一服务区
处北偏东45°方向有一服务区![]() ,且
,且![]() 位于
位于![]() ,
,![]() 两地中点处.
两地中点处.
(1)求![]() ,
,![]() 两地之间的距离;
两地之间的距离;
(2)校车从![]() 地匀速行驶1小时40分钟到达
地匀速行驶1小时40分钟到达![]() 地,若这段路程限速100千米/时,计算校车是否超速?
地,若这段路程限速100千米/时,计算校车是否超速?
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com