
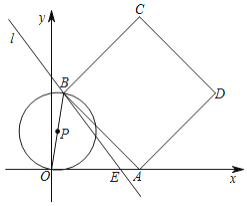
【题目】如图,已知直线![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 为
为![]() 轴上的一个动点(点
轴上的一个动点(点![]() 不与点
不与点![]() 重合),在直线
重合),在直线![]() 上取一点
上取一点![]() (点
(点![]() 在
在![]() 轴上方),使
轴上方),使![]() ,连结
,连结![]() ,以
,以![]() 为边在
为边在![]() 的右侧作正方形
的右侧作正方形![]() ,连结
,连结![]() ,以
,以![]() 为直径作
为直径作![]() .
.
(1)当点![]() 在点
在点![]() 左侧时,若点
左侧时,若点![]() 落在
落在![]() 轴上,则
轴上,则![]() 的长为______,点
的长为______,点![]() 的坐标为_______;
的坐标为_______;
(2)若![]() 与正方形
与正方形![]() 的边相切于点
的边相切于点![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)![]() 与直线
与直线![]() 的交点为
的交点为![]() ,连结
,连结![]() ,当
,当![]() 平分
平分![]() 时,
时,![]() 的长为______.(直接写出答案)
的长为______.(直接写出答案)
【答案】(1)2,![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
(1)先求出直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,进而求出
,进而求出![]() ,得到
,得到![]() ,过点D作DM⊥x轴,得OBADAM,进而即可求解;
,过点D作DM⊥x轴,得OBADAM,进而即可求解;
(2)分3种情况:①如图1,当![]() 与
与![]() 相切于点
相切于点![]() 时,
时,![]() ,点
,点![]() 与点
与点![]() 重合,②如图2,当
重合,②如图2,当![]() 与直线
与直线![]() 相切于点
相切于点![]() ,点
,点![]() 在点
在点![]() 右侧时,则
右侧时,则![]() ,③如图3,,当
,③如图3,,当![]() 与直线
与直线![]() 相切于点
相切于点![]() ,点
,点![]() 在点
在点![]() 左侧时,则
左侧时,则![]() ,分别求解,即可;
,分别求解,即可;
(3)如图4,作![]() 于点
于点![]() ,连结
,连结![]() .设
.设![]() ,可得
,可得![]() ,
,![]() ,
,![]() ,再求出
,再求出![]() ,由条件可知:
,由条件可知:![]() ,
,![]() ,
,![]() 三点共线,列出关于m的比例式,求出m的值,进而即可求解.
三点共线,列出关于m的比例式,求出m的值,进而即可求解.
(1)![]() 直线
直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() .
.
![]() ,
,
![]() ,
,
∵点![]() 在点
在点![]() 左侧,
左侧,
![]() ,
,
如图1,过点D作DM⊥x轴,
∵∠OBA+∠OAB=∠OAB+∠DAM=90°,
∴∠OBA=∠DAM,
又∵AB=DA,∠AOB=∠DMA=90°,
∴OBADAM(AAS),
∴DM=OA=4,OB=AM=8,
∴OM=8+4=12,
![]() ;
;
(2)①如图2,当![]() 与
与![]() 相切于点
相切于点![]() 时,
时,![]() ,
,
又∵∠ABC=90°,点![]() 为
为![]() 轴上的一个动点,
轴上的一个动点,
∴点![]() 与点
与点![]() 重合,
重合,
∴![]() ,
,
设![]() 与x轴的交点为点N,连接BN,则∠BNO=90°,设直线l与y轴交于点K,则OK=8,
与x轴的交点为点N,连接BN,则∠BNO=90°,设直线l与y轴交于点K,则OK=8,
∵BN∥OK,
∴![]() ,即:
,即:![]() ,
,
∴BN=24,NE=18,
∴ON=18-6=12,
∴![]() ;.
;.
②如图3,当![]() 与直线
与直线![]() 相切于点
相切于点![]() ,点
,点![]() 在点
在点![]() 右侧时,则
右侧时,则![]() ,
,
设![]() 与x轴交于点H,连接BH,则∠OHB=90°,
与x轴交于点H,连接BH,则∠OHB=90°,
设![]() ,则
,则![]() ,
,
∵sin∠BEH=![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,即点
,即点![]() 在直线
在直线![]() 上,
上,
联立 ,解得:
,解得: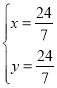
∴点![]() ;
;
③如图4,当![]() 与直线
与直线![]() 相切于点
相切于点![]() ,点
,点![]() 在点
在点![]() 左侧时,则
左侧时,则![]() ,
,
设![]() 与x轴交于点F,连接BF,则∠OFB=90°,
与x轴交于点F,连接BF,则∠OFB=90°,
设![]() ,则
,则![]() ,
,
∵sin∠BEF=![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
![]() ,
,
∴∠ABF+∠OBF=∠BOF+∠OBF=90°,
∴∠ABF=∠BOF,
∵∠AFB=∠BFO=90°,
∴![]() ,
,
∴![]() ,
,
![]() ,解得:
,解得:![]() (舍去),
(舍去),
∴点![]() .
.
综上所述,点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() ;
;
(3)如图5,作![]() 于点
于点![]() ,连结
,连结![]() .
.
设![]() ,则
,则![]() ,
,
由第(2)题,可知![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
过点C作CT⊥GB,交GB的延长线于点T,
∵∠CBT+∠ABG=∠ABG+∠BAG=90°,
∴∠CBT=∠BAG,
又∵∠CTB=∠BGA=90°,CB=BA,
∴CTBBGA(AAS),
∴CT=BG=4m,BT=AG=2m,
∴TG=6m,点C的横坐标=CT-OG=4m-(3m-6)=m+6,
∴![]() ,
,
∵OB是![]() 的直径,
的直径,
∴![]() 直线
直线![]() ,且过原点
,且过原点![]() ,
,
![]() 直线
直线![]() 的解析式为:
的解析式为:![]() ,
,
联立 ,解得:
,解得: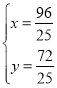 ,
,
![]() .
.
![]() 平分
平分![]() ,
,
![]() ,
,![]() ,
,![]() 三点共线,
三点共线,
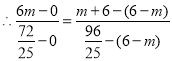 ,解得:
,解得:![]() ,
,
![]() ,
,
![]() .
.
故答案是:![]() .
.


图1 图2
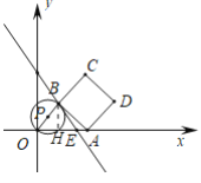

图3 图4
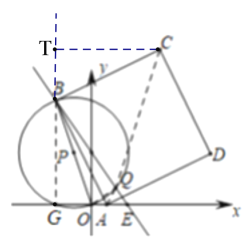
图5


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人分别从A、B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min) 之间的函数关系如图所示.有下列说法: ①A、B之间的距离为1200m;②甲行走的速度是乙的1.5倍;③![]() ;④
;④![]() .以上结论正确的有( )
.以上结论正确的有( )

A.①④B.①②③C.①③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数的图象如图所示,对称轴为x=1,给出下列结论:①abc<0;②b2>4ac;③4a+2b+c<0;④2a+b=0..其中正确的结论有:
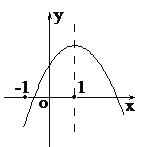
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为圆锥的顶点,M为圆锥底面上一点,点P在OM上.一只蜗牛从P点出发,绕圆锥侧面爬行,回到P点时所爬过的最短路线的痕迹如图所示.若沿OM将圆锥侧面剪开并展开,所得侧面展开图是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
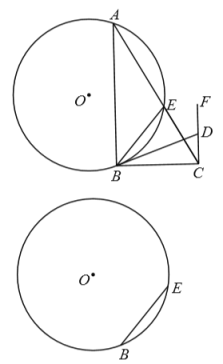
【题目】如图,![]() 是
是![]() 上的两个定点,
上的两个定点,![]() 为优弧
为优弧![]() 上的动点,过点
上的动点,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
(1)求证:![]() 与
与![]() 相切;
相切;
(2)已知:![]()
①若![]() ,求
,求![]() 的长;
的长;
②当![]() 两点间的距离最短时,判断
两点间的距离最短时,判断![]() 四点所组成的四边形的形状,并说明理由.
四点所组成的四边形的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加快城镇化建设,某镇对一条道路进行改造,由甲、乙两工程队合作20天可完成.甲工程队单独施工比乙工程队单独施工多用30天完成此项工程.
(1)求甲、乙两工程队单独完成此项工程各需要多少天?
(2)若甲工程队独做a天后,再由甲、乙两工程队合作施工y天,完成此项工程,试用含a的代数式表示y;
(3)如果甲工程队施工每天需付施工费1万元,乙工程队施工每天需付施工费2.5万元,甲工程队至少要单独施工多少天后,再由甲、乙两工程队合作施工完成剩下的工程,才能使施工费不超过64万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为R的⊙O的弦AC=BD,AC、BD交于E,F为![]() 上一点,连AF、BF、AB、AD,下列结论:①AE=BE;②若AC⊥BD,则AD=
上一点,连AF、BF、AB、AD,下列结论:①AE=BE;②若AC⊥BD,则AD=![]() R;③在②的条件下,若
R;③在②的条件下,若![]() ,AB=
,AB=![]() ,则BF+CE=1.其中正确的是( )
,则BF+CE=1.其中正确的是( )
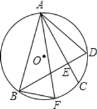
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD的边AB=4,边AD上有一点M,连接BM,将MB绕M点逆时针旋转90°得MN,N恰好落在CD上,过M、D、N作⊙O,⊙O与BC相切,Q为⊙O上的动点,连BQ,P为BQ中点,连AP,则AP的最小值为_____.
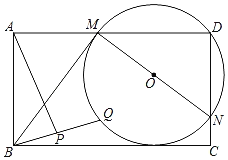
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com