
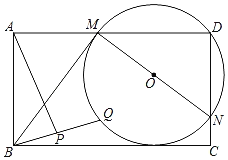
【题目】矩形ABCD的边AB=4,边AD上有一点M,连接BM,将MB绕M点逆时针旋转90°得MN,N恰好落在CD上,过M、D、N作⊙O,⊙O与BC相切,Q为⊙O上的动点,连BQ,P为BQ中点,连AP,则AP的最小值为_____.
【答案】![]() .
.
【解析】
设⊙O与BC的交点为F,连接OB、OF,如图1所示.根据旋转的性质得到MN⊥BM,推出△BMN为等腰直角三角形,由全等三角形的性质得到DM=AB=4,DN=AM,设DN=2a,则AM=2a,OF=4-a,根据勾股定理即可求得⊙O半径,延长BA,使AH=AB=4,连接HQ,OH,过O作OG⊥AB于G,根据三角形中位线的定理得到AP=![]() HQ,HQ∥AP,当HQ取最小值时,AP有最小值,当点Q在HO时,HQ的值最小,根据勾股定理可求得OH,于是可得到结论.
HQ,HQ∥AP,当HQ取最小值时,AP有最小值,当点Q在HO时,HQ的值最小,根据勾股定理可求得OH,于是可得到结论.
设⊙O与BC的交点为F,连接OB、OF,作OR⊥DC于R,如图所示.

∵△MDN为直角三角形,
∴MN为⊙O的直径,
∵将MB绕M点逆时针旋转90°得MN,
∴MN⊥BM,MB=MN,
∴△BMN为等腰直角三角形,
∵∠AMB+∠NMD=180°﹣∠BMN=90°,∠MBA+∠AMB=90°,
∴∠NMD=∠MBA,且BM=NP,∠A=∠NMD=90°,
∴△ABM≌△DMN(AAS),
∴DM=AB=4,DN=AM,
设DN=2a,则AM=2a,OF=4﹣a,
∵OR⊥DC于R,
∴DR=RN=![]() ,
,
∵OR⊥DC,OF⊥BC,∠C=90°,
∴四边形ORCF为矩形,
∴![]() ,
,
BM=![]() ,
,
∵BM=MN=2OF,
∴![]() =
=![]() ,
,
解得:![]() ,
,
∴![]() ,
,![]() =
=![]() ,
,
∴⊙O半径为![]() ,
,
如图2,延长BA,使AH=AB=4,连接HQ,OH,过O作OG⊥AB于G,
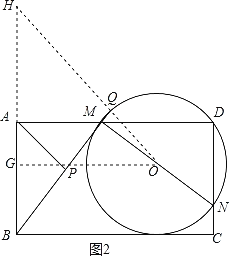
∵AB=AH,BP=PQ,
∴AP=![]() HQ,HQ∥AP,
HQ,HQ∥AP,
∴当HQ取最小值时,AP有最小值,
∴当点Q在HO时,HQ的值最小,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴HQ的最小值=![]() ,
,
∴AP的最小值为![]() ,
,
故答案为:![]() .
.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
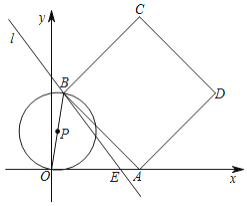
【题目】如图,已知直线![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 为
为![]() 轴上的一个动点(点
轴上的一个动点(点![]() 不与点
不与点![]() 重合),在直线
重合),在直线![]() 上取一点
上取一点![]() (点
(点![]() 在
在![]() 轴上方),使
轴上方),使![]() ,连结
,连结![]() ,以
,以![]() 为边在
为边在![]() 的右侧作正方形
的右侧作正方形![]() ,连结
,连结![]() ,以
,以![]() 为直径作
为直径作![]() .
.
(1)当点![]() 在点
在点![]() 左侧时,若点
左侧时,若点![]() 落在
落在![]() 轴上,则
轴上,则![]() 的长为______,点
的长为______,点![]() 的坐标为_______;
的坐标为_______;
(2)若![]() 与正方形
与正方形![]() 的边相切于点
的边相切于点![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)![]() 与直线
与直线![]() 的交点为
的交点为![]() ,连结
,连结![]() ,当
,当![]() 平分
平分![]() 时,
时,![]() 的长为______.(直接写出答案)
的长为______.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角△ABC中,AB=AC,边BC长为6,高AD长为4,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,则正方形PQMN的边长为( )
A.![]() B.
B.![]() 或
或![]()
C.![]() 或
或![]() D.
D.![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数![]() 的图象的对称轴为直线
的图象的对称轴为直线![]() .
.
(1)求![]() 的值;
的值;
(2)将函数![]() 的图象向右平移2个单位,得到新的函数图象
的图象向右平移2个单位,得到新的函数图象![]() .
.
①直接写出函数图象![]() 的表达式;
的表达式;
②设直线![]() 与
与![]() 轴交于点A,与y轴交于点B,当线段AB与图象
轴交于点A,与y轴交于点B,当线段AB与图象![]() 只有一个公共点时,直接写出
只有一个公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 抛物线
抛物线![]() 经过点
经过点![]() 、
、![]() .
.
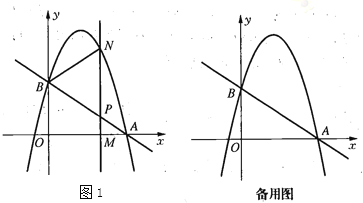
(1)求点![]() 的坐标和抛物线的解析式.
的坐标和抛物线的解析式.
(2)![]() 为
为![]() 轴上一个动点,过点
轴上一个动点,过点![]() 垂直于
垂直于![]() 轴的直线与直线
轴的直线与直线![]() 和抛物线分别交于点
和抛物线分别交于点![]() 、
、![]() .
.
①点![]() 在线段
在线段![]() 上运动,若以
上运动,若以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标;
的坐标;
②点![]() 在
在![]() 轴上自由运动,若三个点
轴上自由运动,若三个点![]() 、
、![]() 、
、![]() 中恰有一点是其他两点所连线段的中点(三点重合除外),则称
中恰有一点是其他两点所连线段的中点(三点重合除外),则称![]() 、
、![]() 、
、![]() 三点为“共谐点”.请直接写出使得
三点为“共谐点”.请直接写出使得![]() 、
、![]() 、
、![]() 三点成为“共谐点”的
三点成为“共谐点”的![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
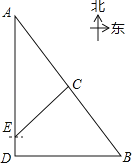
【题目】某校组织学生到恩格贝![]() 和康镇
和康镇![]() 进行研学活动,澄澄老师在网上查得,
进行研学活动,澄澄老师在网上查得,![]() 和
和![]() 分别位于学校
分别位于学校![]() 的正北和正东方向,
的正北和正东方向,![]() 位于
位于![]() 南偏东37°方向,校车从
南偏东37°方向,校车从![]() 出发,沿正北方向前往
出发,沿正北方向前往![]() 地,行驶到15千米的
地,行驶到15千米的![]() 处时,导航显示,在
处时,导航显示,在![]() 处北偏东45°方向有一服务区
处北偏东45°方向有一服务区![]() ,且
,且![]() 位于
位于![]() ,
,![]() 两地中点处.
两地中点处.
(1)求![]() ,
,![]() 两地之间的距离;
两地之间的距离;
(2)校车从![]() 地匀速行驶1小时40分钟到达
地匀速行驶1小时40分钟到达![]() 地,若这段路程限速100千米/时,计算校车是否超速?
地,若这段路程限速100千米/时,计算校车是否超速?
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
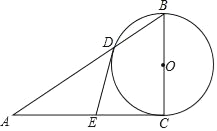
【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
(1)求证:∠A=∠ADE;
(2)若AD=8,DE=5,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
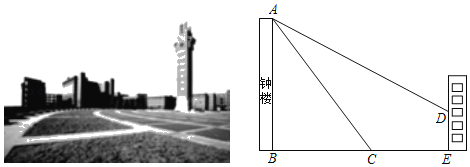
【题目】第十一届全国少数民族传统体育运动会于2019年9月8日至16日在郑州举行,据了解,该赛事每四年举办一届,是我国规格最高、规模最大的综合性民族体育盛会.其中,花炮、押加、民族式摔跤三个项目的比赛在郑州大学主校区进行.如图,钟楼是郑州大学主校区标志性建筑物之一,是郑大的“第一高度”,寓意来自五湖四海的郑大人的团结和凝聚.小刚站在钟楼前C处测得钟楼顶A的仰角为53°,小强站在对面的教学楼三楼上的D处测得钟楼顶A的仰角为30°,此时,两人的水平距离EC为38m.已知教学楼三楼所在的高度为10m,根据测得的数据,计算钟楼AB的高度.(结果保留整数.参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() ,
,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论:①b2﹣4ac<0;②abc>0;③a﹣b+c<0;④m>﹣2,其中,正确的个数有( )

A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com